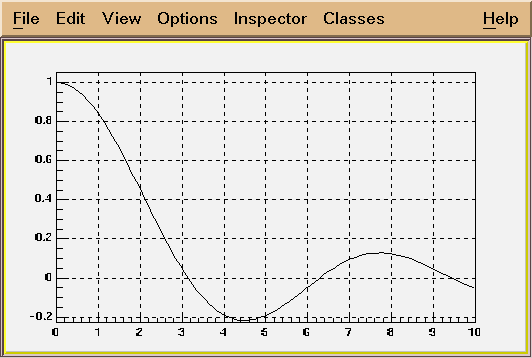
 */
//
//
// Example of a function of type B
// TF1 *f1 = new TF1("f1","[0]*x*sin([1]*x)",-3,3);
// This creates a function of variable x with 2 parameters.
// The parameters must be initialized via:
// f1->SetParameter(0,value_first_parameter);
// f1->SetParameter(1,value_second_parameter);
// Parameters may be given a name:
// f1->SetParName(0,"Constant");
//
// Example of function of type C
// Consider the macro myfunc.C below
//-------------macro myfunc.C-----------------------------
//Double_t myfunction(Double_t *x, Double_t *par)
//{
// Float_t xx =x[0];
// Double_t f = TMath::Abs(par[0]*sin(par[1]*xx)/xx);
// return f;
//}
//void myfunc()
//{
// TF1 *f1 = new TF1("myfunc",myfunction,0,10,2);
// f1->SetParameters(2,1);
// f1->SetParNames("constant","coefficient");
// f1->Draw();
//}
//void myfit()
//{
// TH1F *h1=new TH1F("h1","test",100,0,10);
// h1->FillRandom("myfunc",20000);
// TF1 *f1=gROOT->GetFunction("myfunc");
// f1->SetParameters(800,1);
// h1.Fit("myfunc");
//}
//--------end of macro myfunc.C---------------------------------
//
// In an interactive session you can do:
// Root > .L myfunc.C
// Root > myfunc();
// Root > myfit();
//
//______________________________________________________________________________
TF1::TF1(): TFormula(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*F1 default constructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ======================
fType = 0;
fFunction = 0;
fParErrors = 0;
fParMin = 0;
fParMax = 0;
fChisquare = 0;
fIntegral = 0;
fParent = 0;
fNpfits = 0;
fNsave = 0;
fSave = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
}
//______________________________________________________________________________
TF1::TF1(const char *name,const char *formula, Float_t xmin, Float_t xmax)
:TFormula(name,formula), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*F1 constructor using a formula definition*-*-*-*-*-*-*-*-*-*-*
//*-* =========================================
//*-*
//*-* See TFormula constructor for explanation of the formula syntax.
//*-*
//*-* See tutorials: fillrandom, first, fit1, formula1, multifit
//*-* for real examples.
//*-*
//*-* Creates a function of type A or B between xmin and xmax
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fXmin = xmin;
fXmax = xmax;
fNpx = 100;
fType = 0;
fFunction = 0;
if (fNpar) {
fParErrors = new Double_t[fNpar];
fParMin = new Double_t[fNpar];
fParMax = new Double_t[fNpar];
for (int i = 0; i < fNpar; i++) {
fParErrors[i] = 0;
fParMin[i] = 0;
fParMax[i] = 0;
}
} else {
fParErrors = 0;
fParMin = 0;
fParMax = 0;
}
fChisquare = 0;
fIntegral = 0;
fParent = 0;
fNpfits = 0;
fNsave = 0;
fSave = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
if (!gStyle) return;
SetLineColor(gStyle->GetFuncColor());
SetLineWidth(gStyle->GetFuncWidth());
SetLineStyle(gStyle->GetFuncStyle());
}
//______________________________________________________________________________
TF1::TF1(const char *name,void *fcn, Float_t xmin, Float_t xmax, Int_t npar)
:TFormula(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*F1 constructor using pointer to an interpreted function*-*-*-*
//*-* =======================================================
//*-*
//*-* See TFormula constructor for explanation of the formula syntax.
//*-*
//*-* Creates a function of type C between xmin and xmax.
//*-* The function is defined with npar parameters
//*-* fcn must be a function of type:
//*-* Double_t fcn(Double_t *x, Double_t *params)
//*-*
//*-* see tutorial; myfit for an example of use
//*-* also test/stress.cxx (see function stress1)
//*-*
//*-*
//*-* This constructor is called for functions of type C by CINT.
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fXmin = xmin;
fXmax = xmax;
fNpx = 100;
fType = 2;
fFunction = 0;
if (npar > 0 ) fNpar = npar;
if (fNpar) {
fNames = new TString[fNpar];
fParams = new Double_t[fNpar];
fParErrors = new Double_t[fNpar];
fParMin = new Double_t[fNpar];
fParMax = new Double_t[fNpar];
for (int i = 0; i < fNpar; i++) {
fParams[i] = 0;
fParErrors[i] = 0;
fParMin[i] = 0;
fParMax[i] = 0;
}
} else {
fParErrors = 0;
fParMin = 0;
fParMax = 0;
}
fChisquare = 0;
fIntegral = 0;
fParent = 0;
fNpfits = 0;
fNsave = 0;
fSave = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
fNdim = 1;
if (!fcn) return;
TF1 *f1old = (TF1*)gROOT->GetListOfFunctions()->FindObject(name);
if (f1old) delete f1old;
char *funcname = G__p2f2funcname(fcn);
if (funcname) {
fMethodCall = new TMethodCall();
fMethodCall->InitWithPrototype(funcname,"Double_t*,Double_t*");
fNumber = -1;
} else {
Printf("Function:%s cannot be compiled",name);
}
SetName(name);
SetTitle(funcname);
gROOT->GetListOfFunctions()->Add(this);
if (!gStyle) return;
SetLineColor(gStyle->GetFuncColor());
SetLineWidth(gStyle->GetFuncWidth());
SetLineStyle(gStyle->GetFuncStyle());
}
//______________________________________________________________________________
TF1::TF1(const char *name,Double_t (*fcn)(Double_t *, Double_t *), Float_t xmin, Float_t xmax, Int_t npar)
:TFormula(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*F1 constructor using a pointer to real function*-*-*-*-*-*-*-*
//*-* ===============================================
//*-*
//*-* npar is the number of free parameters used by the function
//*-*
//*-* This constructor creates a function of type C when invoked
//*-* with the normal C++ compiler.
//*-*
//*-* see test program test/stress.cxx (function stress1) for an example.
//*-* note the interface with an intermediate pointer.
//*-*
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fXmin = xmin;
fXmax = xmax;
fNpx = 100;
fType = 1;
fFunction = fcn;
if (npar > 0 ) fNpar = npar;
if (fNpar) {
fNames = new TString[fNpar];
fParams = new Double_t[fNpar];
fParErrors = new Double_t[fNpar];
fParMin = new Double_t[fNpar];
fParMax = new Double_t[fNpar];
for (int i = 0; i < fNpar; i++) {
fParams[i] = 0;
fParErrors[i] = 0;
fParMin[i] = 0;
fParMax[i] = 0;
}
} else {
fParErrors = 0;
fParMin = 0;
fParMax = 0;
}
fChisquare = 0;
fIntegral = 0;
fNsave = 0;
fSave = 0;
fParent = 0;
fNpfits = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
fNdim = 1;
//*-*- Store formula in linked list of formula in ROOT
SetName((char *)name);
if (gROOT->GetListOfFunctions()->FindObject(name)) return;
gROOT->GetListOfFunctions()->Add(this);
if (!gStyle) return;
SetLineColor(gStyle->GetFuncColor());
SetLineWidth(gStyle->GetFuncWidth());
SetLineStyle(gStyle->GetFuncStyle());
}
//______________________________________________________________________________
TF1::~TF1()
{
//*-*-*-*-*-*-*-*-*-*-*F1 default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =====================
if (fParMin) delete [] fParMin;
if (fParMax) delete [] fParMax;
if (fParErrors) delete [] fParErrors;
if (fIntegral) delete [] fIntegral;
if (fSave) delete [] fSave;
delete fHistogram;
delete fMethodCall;
if (fParent) {
if (fParent->InheritsFrom(TH1::Class())) {
((TH1*)fParent)->GetListOfFunctions()->Remove(this);
return;
}
if (fParent->InheritsFrom("TGraph")) {
((TGraph*)fParent)->GetListOfFunctions()->Remove(this);
return;
}
fParent = 0;
}
}
//______________________________________________________________________________
TF1::TF1(const TF1 &f1)
{
((TF1&)f1).Copy(*this);
}
//______________________________________________________________________________
void TF1::Browse(TBrowser *)
{
Draw();
gPad->Update();
}
//______________________________________________________________________________
void TF1::Copy(TObject &obj)
{
//*-*-*-*-*-*-*-*-*-*-*Copy this F1 to a new F1*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
TFormula::Copy(obj);
TAttLine::Copy((TF1&)obj);
TAttFill::Copy((TF1&)obj);
TAttMarker::Copy((TF1&)obj);
((TF1&)obj).fXmin = fXmin;
((TF1&)obj).fXmax = fXmax;
((TF1&)obj).fNpx = fNpx;
((TF1&)obj).fType = fType;
((TF1&)obj).fFunction = fFunction;
((TF1&)obj).fChisquare = fChisquare;
((TF1&)obj).fNpfits = fNpfits;
((TF1&)obj).fMinimum = fMinimum;
((TF1&)obj).fMaximum = fMaximum;
if (fNpar) {
((TF1&)obj).fParErrors = new Double_t[fNpar];
((TF1&)obj).fParMin = new Double_t[fNpar];
((TF1&)obj).fParMax = new Double_t[fNpar];
}
Int_t i;
for (i=0;i<fNpar;i++) ((TF1&)obj).fParErrors[i] = fParErrors[i];
for (i=0;i<fNpar;i++) ((TF1&)obj).fParMin[i] = fParMin[i];
for (i=0;i<fNpar;i++) ((TF1&)obj).fParMax[i] = fParMax[i];
if (fMethodCall) {
TMethodCall *m = new TMethodCall();
m->InitWithPrototype(fMethodCall->GetMethodName(),fMethodCall->GetProto());
((TF1&)obj).fMethodCall = m;
}
}
//______________________________________________________________________________
Double_t TF1::Derivative(Double_t x, Double_t *params, Float_t epsilon)
{
//*-*-*-*-*-*-*-*-*Return derivative of function at point x*-*-*-*-*-*-*-*
//
// The derivative is computed by computing the value of the function
// at point x-epsilon and point x+epsilon.
// if params is NULL, use the current values of parameters
Double_t xx[2];
if (epsilon <= 0) epsilon = 0.001;
epsilon *= fXmax-fXmin;
xx[0] = x - epsilon;
xx[1] = x + epsilon;
if (xx[0] < fXmin) xx[0] = fXmin;
if (xx[1] > fXmax) xx[1] = fXmax;
Double_t f1,f2,deriv;
InitArgs(&xx[0],params);
f1 = EvalPar(&xx[0],params);
InitArgs(&xx[1],params);
f2 = EvalPar(&xx[1],params);
deriv = (f2-f1)/(2*epsilon);
return deriv;
}
//______________________________________________________________________________
Int_t TF1::DistancetoPrimitive(Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a function*-*-*-*-*
//*-* ===============================================
//*-* Compute the closest distance of approach from point px,py to this function.
//*-* The distance is computed in pixels units.
//*-*
//*-* Algorithm:
//*-*
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (!fHistogram) return 9999;
Int_t distance = fHistogram->DistancetoPrimitive(px,py);
if (distance <= 0) return distance;
Double_t xx[1];
Float_t x = gPad->AbsPixeltoX(px);
xx[0] = gPad->PadtoX(x);
Double_t fval = Eval(xx[0]);
Float_t y = gPad->YtoPad(fval);
Int_t pybin = gPad->YtoAbsPixel(y);
return TMath::Abs(py - pybin);
}
//______________________________________________________________________________
void TF1::Draw(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this function with its current attributes*-*-*-*-*
//*-* ==============================================
//*-*
//*-* Possible option values are:
//*-* "SAME" superimpose on top of existing picture
//*-* "L" connect all computed points with a straight line
//*-* "C" connect all computed points with a smooth curve.
//*-*
//*-* Note that the default value is "L". Therefore to draw on top
//*-* of an existing picture, specify option "LSAME"
//*-*
//*-* NB. You must use DrawCopy if you want to draw several times the same
//*-* function in the current canvas.
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
AppendPad(option);
}
//______________________________________________________________________________
TF1 *TF1::DrawCopy(Option_t *option)
{
//*-*-*-*-*-*-*-*Draw a copy of this function with its current attributes*-*-*
//*-* ========================================================
//*-*
//*-* This function MUST be used instead of Draw when you want to draw
//*-* the same function with different parameters settings in the same canvas.
//*-*
//*-* Possible option values are:
//*-* "SAME" superimpose on top of existing picture
//*-* "L" connect all computed points with a straight line
//*-* "C" connect all computed points with a smooth curve.
//*-*
//*-* Note that the default value is "L". Therefore to draw on top
//*-* of an existing picture, specify option "LSAME"
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TF1 *newf1 = new TF1();
Copy(*newf1);
newf1->AppendPad(option);
return newf1;
}
//______________________________________________________________________________
void TF1::DrawF1(const char *formula, Float_t xmin, Float_t xmax, Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*Draw formula between xmin and xmax*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//*-*
if (Compile((char*)formula)) return;
SetRange(xmin, xmax);
Draw(option);
}
//______________________________________________________________________________
void TF1::DrawPanel()
{
//*-*-*-*-*-*-*Display a panel with all function drawing options*-*-*-*-*-*
//*-* =================================================
//*-*
//*-* See class TDrawPanelHist for example
if (gPad) {
//gROOT->SetSelectedPrimitive(gPad->GetSelected());
//gROOT->SetSelectedPad(gPad->GetSelectedPad());
gROOT->SetSelectedPrimitive(this);
gROOT->SetSelectedPad(gPad);
}
TList *lc = (TList*)gROOT->GetListOfCanvases();
if (!lc->FindObject("drawpanelhist")) {
char cmd[] = "TDrawPanelHist *drawpanelhist = new TDrawPanelHist("drawpanelhist","Hist Draw Panel",330,450);";
gInterpreter->ProcessLine(cmd);
return;
}
char cmdupd[] = "drawpanelhist->SetDefaults()";
gInterpreter->ProcessLine(cmdupd);
}
//______________________________________________________________________________
Double_t TF1::Eval(Double_t x, Double_t y, Double_t z)
{
//*-*-*-*-*-*-*-*-*-*-*Evaluate this formula*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =====================
//*-*
//*-* Computes the value of this function (general case for a 3-d function)
//*-* at point x,y,z.
//*-* For a 1-d function give y=0 and z=0
//*-* The current value of variables x,y,z is passed through x, y and z.
//*-* The parameters used will be the ones in the array params if params is given
//*-* otherwise parameters will be taken from the stored data members fParams
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t xx[3];
xx[0] = x;
xx[1] = y;
xx[2] = z;
InitArgs(xx,fParams);
return TF1::EvalPar(xx,fParams);
}
//______________________________________________________________________________
Double_t TF1::EvalPar(Double_t *x, Double_t *params)
{
//*-*-*-*-*-*Evaluate function with given coordinates and parameters*-*-*-*-*-*
//*-* =======================================================
//*-*
// Compute the value of this function at point defined by array x
// and current values of parameters in array params.
// If argument params is omitted or equal 0, the internal values
// of parameters (array fParams) will be used instead.
// For a 1-D function only x[0] must be given.
// In case of a multi-dimemsional function, the arrays x must be
// filled with the corresponding number of dimensions.
//
// WARNING. In case of an interpreted function (fType=2), it is the
// user's responsability to initialize the parameters via InitArgs
// before calling this function.
// InitArgs should be called at least once to specify the addresses
// of the arguments x and params.
// InitArgs should be called everytime these addresses change.
//
if (fType == 0) return TFormula::EvalPar(x,params);
Double_t result = 0;
if (fType == 1) {
if (fFunction) {
if (params) result = (*fFunction)(x,params);
else result = (*fFunction)(x,fParams);
}else result = GetSave(x);
}
if (fType == 2) {
if (fMethodCall) fMethodCall->Execute(result);
else result = GetSave(x);
}
return result;
}
//______________________________________________________________________________
void TF1::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
//*-* =========================================
//*-* This member function is called when a F1 is clicked with the locator
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fHistogram->ExecuteEvent(event,px,py);
if (!gPad->GetView()) {
if (event == kMouseMotion) gPad->SetCursor(kHand);
}
}
//______________________________________________________________________________
TH1F *TF1::GetHistogram()
{
// return a pointer to the histogram used to vusualize the function
if (fHistogram) return fHistogram;
// may be function has not yet be painted. force a pad update
gPad->Modified();
gPad->Update();
return fHistogram;
}
//______________________________________________________________________________
void TF1::GetParLimits(Int_t ipar, Double_t &parmin, Double_t &parmax)
{
//*-*-*-*-*-*Return limits for parameter ipar*-*-*-*
//*-* ================================
parmin = 0;
parmax = 0;
if (ipar < 0 || ipar > fNpar-1) return;
if (fParMin) parmin = fParMin[ipar];
if (fParMax) parmax = fParMax[ipar];
}
//______________________________________________________________________________
Double_t TF1::GetRandom()
{
//*-*-*-*-*-*Return a random number following this function shape*-*-*-*-*-*-*
//*-* ====================================================
//*-*
//*-* The distribution contained in the function fname (TF1) is integrated
//*-* over the channel contents.
//*-* It is normalized to 1.
//*-* Getting one random number implies:
//*-* - Generating a random number between 0 and 1 (say r1)
//*-* - Look in which bin in the normalized integral r1 corresponds to
//*-* - make a linear interpolation in the returned bin
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
// Check if integral array must be build
Int_t i;
Float_t dx = (fXmax-fXmin)/fNpx;
if (fIntegral == 0) {
fIntegral = new Double_t[fNpx+1];
fIntegral[0] = 0;
Double_t integ;
Int_t intNegative = 0;
for (i=0;i<fNpx;i++) {
integ = Integral(fXmin+i*dx, fXmin+i*dx+dx);
if (integ < 0) {intNegative++; integ = -integ;}
fIntegral[i+1] = fIntegral[i] + integ;
}
if (intNegative > 0) {
Warning("GetRandom","function:%s has %d negative values: abs assumed",GetName(),intNegative);
}
if (fIntegral[fNpx] == 0) {
Error("GetRandom","Integral of function is zero");
return 0;
}
for (i=1;i<=fNpx;i++) { // normalize integral to 1
fIntegral[i] /= fIntegral[fNpx];
}
}
// return random number
Float_t r = gRandom->Rndm();
Int_t bin = TMath::BinarySearch(fNpx,fIntegral,r);
Float_t dy = fIntegral[bin+1] - fIntegral[bin];
//printf(" r=%g, bin=%d, dy=%g, dx=%f, I[%d]=%g, I[%d]=%gn",r,bin,dy,dx,bin,fIntegral[bin],bin,fIntegral[bin+1]);
if (dy > 0) return fXmin + (r-fIntegral[bin])*dx/dy +dx*bin;
else return fXmin + dx*bin;
}
//______________________________________________________________________________
void TF1::GetRange(Float_t &xmin, Float_t &xmax)
{
//*-*-*-*-*-*-*-*-*-*-*Return range of a 1-D function*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==============================
xmin = fXmin;
xmax = fXmax;
}
//______________________________________________________________________________
void TF1::GetRange(Float_t &xmin, Float_t &ymin, Float_t &xmax, Float_t &ymax)
{
//*-*-*-*-*-*-*-*-*-*-*Return range of a 2-D function*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==============================
xmin = fXmin;
xmax = fXmax;
ymin = 0;
ymax = 0;
}
//______________________________________________________________________________
void TF1::GetRange(Float_t &xmin, Float_t &ymin, Float_t &zmin, Float_t &xmax, Float_t &ymax, Float_t &zmax)
{
//*-*-*-*-*-*-*-*-*-*-*Return range of function*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
xmin = fXmin;
xmax = fXmax;
ymin = 0;
ymax = 0;
zmin = 0;
zmax = 0;
}
//______________________________________________________________________________
Double_t TF1::GetSave(Double_t *xx)
{
// Get value corresponding to X in array of fSave values
if (fNsave <= 0) return 0;
if (fSave == 0) return 0;
Float_t xmin = Float_t(fSave[fNsave+2]);
Float_t xmax = Float_t(fSave[fNsave+3]);
Float_t x = Float_t(xx[0]);
Float_t dx = (xmax-xmin)/fNsave;
if (x < xmin || x > xmax) return 0;
if (dx <= 0) return 0;
Int_t bin = Int_t((x-xmin)/dx);
Float_t xlow = xmin + bin*dx;
Float_t xup = xlow + dx;
Double_t ylow = fSave[bin];
Double_t yup = fSave[bin+1];
Double_t y = ((xup*ylow-xlow*yup) + x*(yup-ylow))/dx;
return y;
}
//______________________________________________________________________________
void TF1::InitArgs(Double_t *x, Double_t *params)
{
//*-*-*-*-*-*-*-*-*-*-*Initialize parameters addresses*-*-*-*-*-*-*-*-*-*-*-*
//*-* ===============================
if (fMethodCall) {
Long_t args[2];
args[0] = (Long_t)x;
if (params) args[1] = (Long_t)params;
else args[1] = (Long_t)fParams;
fMethodCall->SetParamPtrs(args);
}
}
//______________________________________________________________________________
Double_t TF1::Integral(Float_t a, Float_t b, Double_t *params, Float_t epsilon)
{
//*-*-*-*-*-*-*-*-*Return Integral of function between a and b*-*-*-*-*-*-*-*
//
// based on original CERNLIB routine DGAUSS by Sigfried Kolbig
// converted to C++ by Rene Brun
//
//
/*
*/
//
//
// Example of a function of type B
// TF1 *f1 = new TF1("f1","[0]*x*sin([1]*x)",-3,3);
// This creates a function of variable x with 2 parameters.
// The parameters must be initialized via:
// f1->SetParameter(0,value_first_parameter);
// f1->SetParameter(1,value_second_parameter);
// Parameters may be given a name:
// f1->SetParName(0,"Constant");
//
// Example of function of type C
// Consider the macro myfunc.C below
//-------------macro myfunc.C-----------------------------
//Double_t myfunction(Double_t *x, Double_t *par)
//{
// Float_t xx =x[0];
// Double_t f = TMath::Abs(par[0]*sin(par[1]*xx)/xx);
// return f;
//}
//void myfunc()
//{
// TF1 *f1 = new TF1("myfunc",myfunction,0,10,2);
// f1->SetParameters(2,1);
// f1->SetParNames("constant","coefficient");
// f1->Draw();
//}
//void myfit()
//{
// TH1F *h1=new TH1F("h1","test",100,0,10);
// h1->FillRandom("myfunc",20000);
// TF1 *f1=gROOT->GetFunction("myfunc");
// f1->SetParameters(800,1);
// h1.Fit("myfunc");
//}
//--------end of macro myfunc.C---------------------------------
//
// In an interactive session you can do:
// Root > .L myfunc.C
// Root > myfunc();
// Root > myfit();
//
//______________________________________________________________________________
TF1::TF1(): TFormula(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*F1 default constructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ======================
fType = 0;
fFunction = 0;
fParErrors = 0;
fParMin = 0;
fParMax = 0;
fChisquare = 0;
fIntegral = 0;
fParent = 0;
fNpfits = 0;
fNsave = 0;
fSave = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
}
//______________________________________________________________________________
TF1::TF1(const char *name,const char *formula, Float_t xmin, Float_t xmax)
:TFormula(name,formula), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*F1 constructor using a formula definition*-*-*-*-*-*-*-*-*-*-*
//*-* =========================================
//*-*
//*-* See TFormula constructor for explanation of the formula syntax.
//*-*
//*-* See tutorials: fillrandom, first, fit1, formula1, multifit
//*-* for real examples.
//*-*
//*-* Creates a function of type A or B between xmin and xmax
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fXmin = xmin;
fXmax = xmax;
fNpx = 100;
fType = 0;
fFunction = 0;
if (fNpar) {
fParErrors = new Double_t[fNpar];
fParMin = new Double_t[fNpar];
fParMax = new Double_t[fNpar];
for (int i = 0; i < fNpar; i++) {
fParErrors[i] = 0;
fParMin[i] = 0;
fParMax[i] = 0;
}
} else {
fParErrors = 0;
fParMin = 0;
fParMax = 0;
}
fChisquare = 0;
fIntegral = 0;
fParent = 0;
fNpfits = 0;
fNsave = 0;
fSave = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
if (!gStyle) return;
SetLineColor(gStyle->GetFuncColor());
SetLineWidth(gStyle->GetFuncWidth());
SetLineStyle(gStyle->GetFuncStyle());
}
//______________________________________________________________________________
TF1::TF1(const char *name,void *fcn, Float_t xmin, Float_t xmax, Int_t npar)
:TFormula(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*F1 constructor using pointer to an interpreted function*-*-*-*
//*-* =======================================================
//*-*
//*-* See TFormula constructor for explanation of the formula syntax.
//*-*
//*-* Creates a function of type C between xmin and xmax.
//*-* The function is defined with npar parameters
//*-* fcn must be a function of type:
//*-* Double_t fcn(Double_t *x, Double_t *params)
//*-*
//*-* see tutorial; myfit for an example of use
//*-* also test/stress.cxx (see function stress1)
//*-*
//*-*
//*-* This constructor is called for functions of type C by CINT.
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fXmin = xmin;
fXmax = xmax;
fNpx = 100;
fType = 2;
fFunction = 0;
if (npar > 0 ) fNpar = npar;
if (fNpar) {
fNames = new TString[fNpar];
fParams = new Double_t[fNpar];
fParErrors = new Double_t[fNpar];
fParMin = new Double_t[fNpar];
fParMax = new Double_t[fNpar];
for (int i = 0; i < fNpar; i++) {
fParams[i] = 0;
fParErrors[i] = 0;
fParMin[i] = 0;
fParMax[i] = 0;
}
} else {
fParErrors = 0;
fParMin = 0;
fParMax = 0;
}
fChisquare = 0;
fIntegral = 0;
fParent = 0;
fNpfits = 0;
fNsave = 0;
fSave = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
fNdim = 1;
if (!fcn) return;
TF1 *f1old = (TF1*)gROOT->GetListOfFunctions()->FindObject(name);
if (f1old) delete f1old;
char *funcname = G__p2f2funcname(fcn);
if (funcname) {
fMethodCall = new TMethodCall();
fMethodCall->InitWithPrototype(funcname,"Double_t*,Double_t*");
fNumber = -1;
} else {
Printf("Function:%s cannot be compiled",name);
}
SetName(name);
SetTitle(funcname);
gROOT->GetListOfFunctions()->Add(this);
if (!gStyle) return;
SetLineColor(gStyle->GetFuncColor());
SetLineWidth(gStyle->GetFuncWidth());
SetLineStyle(gStyle->GetFuncStyle());
}
//______________________________________________________________________________
TF1::TF1(const char *name,Double_t (*fcn)(Double_t *, Double_t *), Float_t xmin, Float_t xmax, Int_t npar)
:TFormula(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*F1 constructor using a pointer to real function*-*-*-*-*-*-*-*
//*-* ===============================================
//*-*
//*-* npar is the number of free parameters used by the function
//*-*
//*-* This constructor creates a function of type C when invoked
//*-* with the normal C++ compiler.
//*-*
//*-* see test program test/stress.cxx (function stress1) for an example.
//*-* note the interface with an intermediate pointer.
//*-*
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fXmin = xmin;
fXmax = xmax;
fNpx = 100;
fType = 1;
fFunction = fcn;
if (npar > 0 ) fNpar = npar;
if (fNpar) {
fNames = new TString[fNpar];
fParams = new Double_t[fNpar];
fParErrors = new Double_t[fNpar];
fParMin = new Double_t[fNpar];
fParMax = new Double_t[fNpar];
for (int i = 0; i < fNpar; i++) {
fParams[i] = 0;
fParErrors[i] = 0;
fParMin[i] = 0;
fParMax[i] = 0;
}
} else {
fParErrors = 0;
fParMin = 0;
fParMax = 0;
}
fChisquare = 0;
fIntegral = 0;
fNsave = 0;
fSave = 0;
fParent = 0;
fNpfits = 0;
fHistogram = 0;
fMinimum = -1111;
fMaximum = -1111;
fMethodCall = 0;
fNdim = 1;
//*-*- Store formula in linked list of formula in ROOT
SetName((char *)name);
if (gROOT->GetListOfFunctions()->FindObject(name)) return;
gROOT->GetListOfFunctions()->Add(this);
if (!gStyle) return;
SetLineColor(gStyle->GetFuncColor());
SetLineWidth(gStyle->GetFuncWidth());
SetLineStyle(gStyle->GetFuncStyle());
}
//______________________________________________________________________________
TF1::~TF1()
{
//*-*-*-*-*-*-*-*-*-*-*F1 default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =====================
if (fParMin) delete [] fParMin;
if (fParMax) delete [] fParMax;
if (fParErrors) delete [] fParErrors;
if (fIntegral) delete [] fIntegral;
if (fSave) delete [] fSave;
delete fHistogram;
delete fMethodCall;
if (fParent) {
if (fParent->InheritsFrom(TH1::Class())) {
((TH1*)fParent)->GetListOfFunctions()->Remove(this);
return;
}
if (fParent->InheritsFrom("TGraph")) {
((TGraph*)fParent)->GetListOfFunctions()->Remove(this);
return;
}
fParent = 0;
}
}
//______________________________________________________________________________
TF1::TF1(const TF1 &f1)
{
((TF1&)f1).Copy(*this);
}
//______________________________________________________________________________
void TF1::Browse(TBrowser *)
{
Draw();
gPad->Update();
}
//______________________________________________________________________________
void TF1::Copy(TObject &obj)
{
//*-*-*-*-*-*-*-*-*-*-*Copy this F1 to a new F1*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
TFormula::Copy(obj);
TAttLine::Copy((TF1&)obj);
TAttFill::Copy((TF1&)obj);
TAttMarker::Copy((TF1&)obj);
((TF1&)obj).fXmin = fXmin;
((TF1&)obj).fXmax = fXmax;
((TF1&)obj).fNpx = fNpx;
((TF1&)obj).fType = fType;
((TF1&)obj).fFunction = fFunction;
((TF1&)obj).fChisquare = fChisquare;
((TF1&)obj).fNpfits = fNpfits;
((TF1&)obj).fMinimum = fMinimum;
((TF1&)obj).fMaximum = fMaximum;
if (fNpar) {
((TF1&)obj).fParErrors = new Double_t[fNpar];
((TF1&)obj).fParMin = new Double_t[fNpar];
((TF1&)obj).fParMax = new Double_t[fNpar];
}
Int_t i;
for (i=0;i<fNpar;i++) ((TF1&)obj).fParErrors[i] = fParErrors[i];
for (i=0;i<fNpar;i++) ((TF1&)obj).fParMin[i] = fParMin[i];
for (i=0;i<fNpar;i++) ((TF1&)obj).fParMax[i] = fParMax[i];
if (fMethodCall) {
TMethodCall *m = new TMethodCall();
m->InitWithPrototype(fMethodCall->GetMethodName(),fMethodCall->GetProto());
((TF1&)obj).fMethodCall = m;
}
}
//______________________________________________________________________________
Double_t TF1::Derivative(Double_t x, Double_t *params, Float_t epsilon)
{
//*-*-*-*-*-*-*-*-*Return derivative of function at point x*-*-*-*-*-*-*-*
//
// The derivative is computed by computing the value of the function
// at point x-epsilon and point x+epsilon.
// if params is NULL, use the current values of parameters
Double_t xx[2];
if (epsilon <= 0) epsilon = 0.001;
epsilon *= fXmax-fXmin;
xx[0] = x - epsilon;
xx[1] = x + epsilon;
if (xx[0] < fXmin) xx[0] = fXmin;
if (xx[1] > fXmax) xx[1] = fXmax;
Double_t f1,f2,deriv;
InitArgs(&xx[0],params);
f1 = EvalPar(&xx[0],params);
InitArgs(&xx[1],params);
f2 = EvalPar(&xx[1],params);
deriv = (f2-f1)/(2*epsilon);
return deriv;
}
//______________________________________________________________________________
Int_t TF1::DistancetoPrimitive(Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a function*-*-*-*-*
//*-* ===============================================
//*-* Compute the closest distance of approach from point px,py to this function.
//*-* The distance is computed in pixels units.
//*-*
//*-* Algorithm:
//*-*
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
if (!fHistogram) return 9999;
Int_t distance = fHistogram->DistancetoPrimitive(px,py);
if (distance <= 0) return distance;
Double_t xx[1];
Float_t x = gPad->AbsPixeltoX(px);
xx[0] = gPad->PadtoX(x);
Double_t fval = Eval(xx[0]);
Float_t y = gPad->YtoPad(fval);
Int_t pybin = gPad->YtoAbsPixel(y);
return TMath::Abs(py - pybin);
}
//______________________________________________________________________________
void TF1::Draw(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this function with its current attributes*-*-*-*-*
//*-* ==============================================
//*-*
//*-* Possible option values are:
//*-* "SAME" superimpose on top of existing picture
//*-* "L" connect all computed points with a straight line
//*-* "C" connect all computed points with a smooth curve.
//*-*
//*-* Note that the default value is "L". Therefore to draw on top
//*-* of an existing picture, specify option "LSAME"
//*-*
//*-* NB. You must use DrawCopy if you want to draw several times the same
//*-* function in the current canvas.
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TString opt = option;
opt.ToLower();
if (gPad && !opt.Contains("same")) gPad->Clear();
AppendPad(option);
}
//______________________________________________________________________________
TF1 *TF1::DrawCopy(Option_t *option)
{
//*-*-*-*-*-*-*-*Draw a copy of this function with its current attributes*-*-*
//*-* ========================================================
//*-*
//*-* This function MUST be used instead of Draw when you want to draw
//*-* the same function with different parameters settings in the same canvas.
//*-*
//*-* Possible option values are:
//*-* "SAME" superimpose on top of existing picture
//*-* "L" connect all computed points with a straight line
//*-* "C" connect all computed points with a smooth curve.
//*-*
//*-* Note that the default value is "L". Therefore to draw on top
//*-* of an existing picture, specify option "LSAME"
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
TF1 *newf1 = new TF1();
Copy(*newf1);
newf1->AppendPad(option);
return newf1;
}
//______________________________________________________________________________
void TF1::DrawF1(const char *formula, Float_t xmin, Float_t xmax, Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*Draw formula between xmin and xmax*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//*-*
if (Compile((char*)formula)) return;
SetRange(xmin, xmax);
Draw(option);
}
//______________________________________________________________________________
void TF1::DrawPanel()
{
//*-*-*-*-*-*-*Display a panel with all function drawing options*-*-*-*-*-*
//*-* =================================================
//*-*
//*-* See class TDrawPanelHist for example
if (gPad) {
//gROOT->SetSelectedPrimitive(gPad->GetSelected());
//gROOT->SetSelectedPad(gPad->GetSelectedPad());
gROOT->SetSelectedPrimitive(this);
gROOT->SetSelectedPad(gPad);
}
TList *lc = (TList*)gROOT->GetListOfCanvases();
if (!lc->FindObject("drawpanelhist")) {
char cmd[] = "TDrawPanelHist *drawpanelhist = new TDrawPanelHist("drawpanelhist","Hist Draw Panel",330,450);";
gInterpreter->ProcessLine(cmd);
return;
}
char cmdupd[] = "drawpanelhist->SetDefaults()";
gInterpreter->ProcessLine(cmdupd);
}
//______________________________________________________________________________
Double_t TF1::Eval(Double_t x, Double_t y, Double_t z)
{
//*-*-*-*-*-*-*-*-*-*-*Evaluate this formula*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =====================
//*-*
//*-* Computes the value of this function (general case for a 3-d function)
//*-* at point x,y,z.
//*-* For a 1-d function give y=0 and z=0
//*-* The current value of variables x,y,z is passed through x, y and z.
//*-* The parameters used will be the ones in the array params if params is given
//*-* otherwise parameters will be taken from the stored data members fParams
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Double_t xx[3];
xx[0] = x;
xx[1] = y;
xx[2] = z;
InitArgs(xx,fParams);
return TF1::EvalPar(xx,fParams);
}
//______________________________________________________________________________
Double_t TF1::EvalPar(Double_t *x, Double_t *params)
{
//*-*-*-*-*-*Evaluate function with given coordinates and parameters*-*-*-*-*-*
//*-* =======================================================
//*-*
// Compute the value of this function at point defined by array x
// and current values of parameters in array params.
// If argument params is omitted or equal 0, the internal values
// of parameters (array fParams) will be used instead.
// For a 1-D function only x[0] must be given.
// In case of a multi-dimemsional function, the arrays x must be
// filled with the corresponding number of dimensions.
//
// WARNING. In case of an interpreted function (fType=2), it is the
// user's responsability to initialize the parameters via InitArgs
// before calling this function.
// InitArgs should be called at least once to specify the addresses
// of the arguments x and params.
// InitArgs should be called everytime these addresses change.
//
if (fType == 0) return TFormula::EvalPar(x,params);
Double_t result = 0;
if (fType == 1) {
if (fFunction) {
if (params) result = (*fFunction)(x,params);
else result = (*fFunction)(x,fParams);
}else result = GetSave(x);
}
if (fType == 2) {
if (fMethodCall) fMethodCall->Execute(result);
else result = GetSave(x);
}
return result;
}
//______________________________________________________________________________
void TF1::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
//*-* =========================================
//*-* This member function is called when a F1 is clicked with the locator
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
fHistogram->ExecuteEvent(event,px,py);
if (!gPad->GetView()) {
if (event == kMouseMotion) gPad->SetCursor(kHand);
}
}
//______________________________________________________________________________
TH1F *TF1::GetHistogram()
{
// return a pointer to the histogram used to vusualize the function
if (fHistogram) return fHistogram;
// may be function has not yet be painted. force a pad update
gPad->Modified();
gPad->Update();
return fHistogram;
}
//______________________________________________________________________________
void TF1::GetParLimits(Int_t ipar, Double_t &parmin, Double_t &parmax)
{
//*-*-*-*-*-*Return limits for parameter ipar*-*-*-*
//*-* ================================
parmin = 0;
parmax = 0;
if (ipar < 0 || ipar > fNpar-1) return;
if (fParMin) parmin = fParMin[ipar];
if (fParMax) parmax = fParMax[ipar];
}
//______________________________________________________________________________
Double_t TF1::GetRandom()
{
//*-*-*-*-*-*Return a random number following this function shape*-*-*-*-*-*-*
//*-* ====================================================
//*-*
//*-* The distribution contained in the function fname (TF1) is integrated
//*-* over the channel contents.
//*-* It is normalized to 1.
//*-* Getting one random number implies:
//*-* - Generating a random number between 0 and 1 (say r1)
//*-* - Look in which bin in the normalized integral r1 corresponds to
//*-* - make a linear interpolation in the returned bin
//*-*
//*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*
// Check if integral array must be build
Int_t i;
Float_t dx = (fXmax-fXmin)/fNpx;
if (fIntegral == 0) {
fIntegral = new Double_t[fNpx+1];
fIntegral[0] = 0;
Double_t integ;
Int_t intNegative = 0;
for (i=0;i<fNpx;i++) {
integ = Integral(fXmin+i*dx, fXmin+i*dx+dx);
if (integ < 0) {intNegative++; integ = -integ;}
fIntegral[i+1] = fIntegral[i] + integ;
}
if (intNegative > 0) {
Warning("GetRandom","function:%s has %d negative values: abs assumed",GetName(),intNegative);
}
if (fIntegral[fNpx] == 0) {
Error("GetRandom","Integral of function is zero");
return 0;
}
for (i=1;i<=fNpx;i++) { // normalize integral to 1
fIntegral[i] /= fIntegral[fNpx];
}
}
// return random number
Float_t r = gRandom->Rndm();
Int_t bin = TMath::BinarySearch(fNpx,fIntegral,r);
Float_t dy = fIntegral[bin+1] - fIntegral[bin];
//printf(" r=%g, bin=%d, dy=%g, dx=%f, I[%d]=%g, I[%d]=%gn",r,bin,dy,dx,bin,fIntegral[bin],bin,fIntegral[bin+1]);
if (dy > 0) return fXmin + (r-fIntegral[bin])*dx/dy +dx*bin;
else return fXmin + dx*bin;
}
//______________________________________________________________________________
void TF1::GetRange(Float_t &xmin, Float_t &xmax)
{
//*-*-*-*-*-*-*-*-*-*-*Return range of a 1-D function*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==============================
xmin = fXmin;
xmax = fXmax;
}
//______________________________________________________________________________
void TF1::GetRange(Float_t &xmin, Float_t &ymin, Float_t &xmax, Float_t &ymax)
{
//*-*-*-*-*-*-*-*-*-*-*Return range of a 2-D function*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==============================
xmin = fXmin;
xmax = fXmax;
ymin = 0;
ymax = 0;
}
//______________________________________________________________________________
void TF1::GetRange(Float_t &xmin, Float_t &ymin, Float_t &zmin, Float_t &xmax, Float_t &ymax, Float_t &zmax)
{
//*-*-*-*-*-*-*-*-*-*-*Return range of function*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
xmin = fXmin;
xmax = fXmax;
ymin = 0;
ymax = 0;
zmin = 0;
zmax = 0;
}
//______________________________________________________________________________
Double_t TF1::GetSave(Double_t *xx)
{
// Get value corresponding to X in array of fSave values
if (fNsave <= 0) return 0;
if (fSave == 0) return 0;
Float_t xmin = Float_t(fSave[fNsave+2]);
Float_t xmax = Float_t(fSave[fNsave+3]);
Float_t x = Float_t(xx[0]);
Float_t dx = (xmax-xmin)/fNsave;
if (x < xmin || x > xmax) return 0;
if (dx <= 0) return 0;
Int_t bin = Int_t((x-xmin)/dx);
Float_t xlow = xmin + bin*dx;
Float_t xup = xlow + dx;
Double_t ylow = fSave[bin];
Double_t yup = fSave[bin+1];
Double_t y = ((xup*ylow-xlow*yup) + x*(yup-ylow))/dx;
return y;
}
//______________________________________________________________________________
void TF1::InitArgs(Double_t *x, Double_t *params)
{
//*-*-*-*-*-*-*-*-*-*-*Initialize parameters addresses*-*-*-*-*-*-*-*-*-*-*-*
//*-* ===============================
if (fMethodCall) {
Long_t args[2];
args[0] = (Long_t)x;
if (params) args[1] = (Long_t)params;
else args[1] = (Long_t)fParams;
fMethodCall->SetParamPtrs(args);
}
}
//______________________________________________________________________________
Double_t TF1::Integral(Float_t a, Float_t b, Double_t *params, Float_t epsilon)
{
//*-*-*-*-*-*-*-*-*Return Integral of function between a and b*-*-*-*-*-*-*-*
//
// based on original CERNLIB routine DGAUSS by Sigfried Kolbig
// converted to C++ by Rene Brun
//
//
/*
This function computes, to an attempted specified accuracy, the value of the integral
![]()
Usage:
In any arithmetic expression, this function has the approximate value of the integral I.
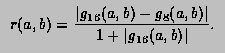
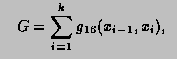
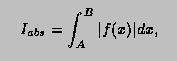
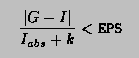
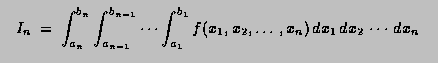 */
//
//
// Author(s): A.C. Genz, A.A. Malik
// converted/adaptedted by R.Brun to C++ from Fortran CERNLIB routine RADMUL (D120)
// The new code features many changes compared to the Fortran version.
// Note that this function is currently called only by TF2::Integral (n=2)
// and TF3::Integral (n=3).
//
// This function computes, to an attempted specified accuracy, the value of
// the integral over an n-dimensional rectangular region.
//
// N Number of dimensions.
// A,B One-dimensional arrays of length >= N . On entry A[i], and B[i],
// contain the lower and upper limits of integration, respectively.
// EPS Specified relative accuracy.
// RELERR Contains, on exit, an estimation of the relative accuray of RESULT.
//
// Method:
//
// An integration rule of degree seven is used together with a certain
// strategy of subdivision.
// For a more detailed description of the method see References.
//
// Notes:
//
// 1.Multi-dimensional integration is time-consuming. For each rectangular
// subregion, the routine requires function evaluations.
// Careful programming of the integrand might result in substantial saving
// of time.
// 2.Numerical integration usually works best for smooth functions.
// Some analysis or suitable transformations of the integral prior to
// numerical work may contribute to numerical efficiency.
//
// References:
//
// 1.A.C. Genz and A.A. Malik, Remarks on algorithm 006:
// An adaptive algorithm for numerical integration over
// an N-dimensional rectangular region, J. Comput. Appl. Math. 6 (1980) 295-302.
// 2.A. van Doren and L. de Ridder, An adaptive algorithm for numerical
// integration over an n-dimensional cube, J.Comput. Appl. Math. 2 (1976) 207-217.
//
//=========================================================================
Double_t ctr[15], wth[15], wthl[15], z[15];
const Double_t xl2 = 0.358568582800318073;
const Double_t xl4 = 0.948683298050513796;
const Double_t xl5 = 0.688247201611685289;
const Double_t w2 = 980./6561;
const Double_t w4 = 200./19683;
const Double_t wp2 = 245./486;
const Double_t wp4 = 25./729;
Double_t wn1[14] = { -0.193872885230909911, -0.555606360818980835,
-0.876695625666819078, -1.15714067977442459, -1.39694152314179743,
-1.59609815576893754, -1.75461057765584494, -1.87247878880251983,
-1.94970278920896201, -1.98628257887517146, -1.98221815780114818,
-1.93750952598689219, -1.85215668343240347, -1.72615963013768225};
Double_t wn3[14] = { 0.0518213686937966768, 0.0314992633236803330,
0.0111771579535639891,-0.00914494741655235473,-0.0294670527866686986,
-0.0497891581567850424,-0.0701112635269013768, -0.0904333688970177241,
-0.110755474267134071, -0.131077579637250419, -0.151399685007366752,
-0.171721790377483099, -0.192043895747599447, -0.212366001117715794};
Double_t wn5[14] = { 0.871183254585174982e-01, 0.435591627292587508e-01,
0.217795813646293754e-01, 0.108897906823146873e-01, 0.544489534115734364e-02,
0.272244767057867193e-02, 0.136122383528933596e-02, 0.680611917644667955e-03,
0.340305958822333977e-03, 0.170152979411166995e-03, 0.850764897055834977e-04,
0.425382448527917472e-04, 0.212691224263958736e-04, 0.106345612131979372e-04};
Double_t wpn1[14] = { -1.33196159122085045, -2.29218106995884763,
-3.11522633744855959, -3.80109739368998611, -4.34979423868312742,
-4.76131687242798352, -5.03566529492455417, -5.17283950617283939,
-5.17283950617283939, -5.03566529492455417, -4.76131687242798352,
-4.34979423868312742, -3.80109739368998611, -3.11522633744855959};
Double_t wpn3[14] = { 0.0445816186556927292, -0.0240054869684499309,
-0.0925925925925925875, -0.161179698216735251, -0.229766803840877915,
-0.298353909465020564, -0.366941015089163228, -0.435528120713305891,
-0.504115226337448555, -0.572702331961591218, -0.641289437585733882,
-0.709876543209876532, -0.778463648834019195, -0.847050754458161859};
Double_t result = 0;
Double_t abserr = 0;
Int_t ifail = 3;
if (n < 2 || n > 15) return 0;
Double_t twondm = TMath::Power(2,n);
Int_t ifncls = 0;
Bool_t ldv = kFALSE;
Int_t irgnst = 2*n+3;
Int_t irlcls = Int_t(twondm) +2*n*(n+1)+1;
Int_t isbrgn = irgnst;
Int_t isbrgs = irgnst;
// The original algorithm expected a parameter MAXPTS
// where MAXPTS = Maximum number of function evaluations to be allowed.
// Here we set MAXPTS to 2*(the lowest possible value)
Int_t maxpts = 2*irlcls;
Int_t minpts = 1;
// The original agorithm expected a working space array WK of length IWK
// with IWK Length ( >= (2N + 3) * (1 + MAXPTS/(2**N + 2N(N + 1) + 1))/2).
// Here, this array is allocated dynamically
Int_t iwk = irgnst*(1 +maxpts/irlcls)/2;
Double_t *wk = new Double_t[iwk+10];
Int_t j;
for (j=0;j<n;j++) {
ctr[j] = (b[j] + a[j])*0.5;
wth[j] = (b[j] - a[j])*0.5;
}
Double_t rgnvol, sum1, sum2, sum3, sum4, sum5, difmax, f2, f3, dif;
Double_t rgncmp=0, rgnval, rgnerr;
Int_t j1, k, l, m, idvaxn=0, idvax0=0, isbtmp, isbtpp;
InitArgs(z,fParams);
L20:
rgnvol = twondm;
for (j=0;j<n;j++) {
rgnvol *= wth[j];
z[j] = ctr[j];
}
sum1 = EvalPar(z,fParams); //evaluate function
difmax = 0;
sum2 = 0;
sum3 = 0;
for (j=0;j<n;j++) {
z[j] = ctr[j] - xl2*wth[j];
f2 = EvalPar(z,fParams);
z[j] = ctr[j] + xl2*wth[j];
f2 += EvalPar(z,fParams);
wthl[j] = xl4*wth[j];
z[j] = ctr[j] - wthl[j];
f3 = EvalPar(z,fParams);
z[j] = ctr[j] + wthl[j];
f3 += EvalPar(z,fParams);
sum2 += f2;
sum3 += f3;
dif = TMath::Abs(7*f2-f3-12*sum1);
difmax = TMath::Max(dif, difmax);
if (difmax == dif) idvaxn = j+1;
z[j] = ctr[j];
}
sum4 = 0;
for (j=1;j<n;j++) {
j1 = j-1;
for (k=j;k<n;k++) {
for (l=0;l<2;l++) {
wthl[j1] = -wthl[j1];
z[j1] = ctr[j1] + wthl[j1];
for (m=0;m<2;m++) {
wthl[k] = -wthl[k];
z[k] = ctr[k] + wthl[k];
sum4 += EvalPar(z,fParams);
}
}
z[k] = ctr[k];
}
z[j1] = ctr[j1];
}
sum5 = 0;
for (j=0;j<n;j++) {
wthl[j] = -xl5*wth[j];
z[j] = ctr[j] + wthl[j];
}
L90:
sum5 += EvalPar(z,fParams);
for (j=0;j<n;j++) {
wthl[j] = -wthl[j];
z[j] = ctr[j] + wthl[j];
if (wthl[j] > 0) goto L90;
}
rgncmp = rgnvol*(wpn1[n-2]*sum1+wp2*sum2+wpn3[n-2]*sum3+wp4*sum4);
rgnval = wn1[n-2]*sum1+w2*sum2+wn3[n-2]*sum3+w4*sum4+wn5[n-2]*sum5;
rgnval *= rgnvol;
rgnerr = TMath::Abs(rgnval-rgncmp);
result += rgnval;
abserr += rgnerr;
ifncls += irlcls;
if (ldv) {
L110:
isbtmp = 2*isbrgn;
if (isbtmp > isbrgs) goto L160;
if (isbtmp < isbrgs) {
isbtpp = isbtmp + irgnst;
if (wk[isbtmp-1] < wk[isbtpp-1]) isbtmp = isbtpp;
}
if (rgnerr >= wk[isbtmp-1]) goto L160;
for (k=0;k<irgnst;k++) {
wk[isbrgn-k-1] = wk[isbtmp-k-1];
}
isbrgn = isbtmp;
goto L110;
}
L140:
isbtmp = (isbrgn/(2*irgnst))*irgnst;
if (isbtmp >= irgnst && rgnerr > wk[isbtmp-1]) {
for (k=0;k<irgnst;k++) {
wk[isbrgn-k-1] = wk[isbtmp-k-1];
}
isbrgn = isbtmp;
goto L140;
}
L160:
wk[isbrgn-1] = rgnerr;
wk[isbrgn-2] = rgnval;
wk[isbrgn-3] = Double_t(idvaxn);
for (j=0;j<n;j++) {
isbtmp = isbrgn-2*j-4;
wk[isbtmp] = ctr[j];
wk[isbtmp-1] = wth[j];
}
if (ldv) {
ldv = kFALSE;
ctr[idvax0-1] += 2*wth[idvax0-1];
isbrgs += irgnst;
isbrgn = isbrgs;
goto L20;
}
relerr = abserr/TMath::Abs(result);
if (isbrgs+irgnst > iwk) ifail = 2;
if (ifncls+2*irlcls > maxpts) ifail = 1;
if (relerr < eps && ifncls >= minpts) ifail = 0;
if (ifail == 3) {
ldv = kTRUE;
isbrgn = irgnst;
abserr -= wk[isbrgn-1];
result -= wk[isbrgn-2];
idvax0 = Int_t(wk[isbrgn-3]);
for (j=0;j<n;j++) {
isbtmp = isbrgn-2*j-4;
ctr[j] = wk[isbtmp];
wth[j] = wk[isbtmp-1];
}
wth[idvax0-1] = 0.5*wth[idvax0-1];
ctr[idvax0-1] -= wth[idvax0-1];
goto L20;
}
// IFAIL On exit:
// 0 Normal exit. . At most MAXPTS calls to the function F were performed.
// 1 MAXPTS is too small for the specified accuracy EPS. RESULT and RELERR
// contain the values obtainable for the specified value of MAXPTS.
//
delete [] wk;
// Int_t nfnevl = ifncls; //number of function evaluations performed.
return result; //an approximate value of the integral
}
//______________________________________________________________________________
void TF1::Paint(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Paint this function with its current attributes*-*-*-*-*
//*-* ===============================================
const Int_t kLogX = BIT(15);
Int_t i;
Double_t xv[1];
TString opt = option;
opt.ToLower();
Float_t xmin, xmax, pmin, pmax;
pmin = gPad->PadtoX(gPad->GetUxmin());
pmax = gPad->PadtoX(gPad->GetUxmax());
xmin = fXmin;
xmax = fXmax;
if (opt.Contains("same")) {
if (xmax < pmin) return; // Otto: completely outside
if (xmin > pmax) return;
if (xmin < pmin) xmin = pmin;
if (xmax > pmax) xmax = pmax;
} else {
gPad->Clear();
}
//*-*- Create a temporary histogram and fill each channel with the function value
if (fHistogram) {
if (!gPad->GetLogx() && fHistogram->TestBit(kLogX)) { delete fHistogram; fHistogram = 0;}
if ( gPad->GetLogx() && !fHistogram->TestBit(kLogX)) { delete fHistogram; fHistogram = 0;}
}
if (fHistogram) {
if (xmin != fXmin || xmax != fXmax) fHistogram->GetXaxis()->SetLimits(xmin,xmax);
} else {
// if logx, we must bin in logx and not in x !!!
// otherwise if several decades, one gets crazy results
if (xmin > 0 && gPad->GetLogx()) {
Float_t *xbins = new Float_t[fNpx+1];
Float_t xlogmin = TMath::Log10(xmin);
Float_t xlogmax = TMath::Log10(xmax);
Float_t dlogx = (xlogmax-xlogmin)/((Float_t)fNpx);
for (i=0;i<=fNpx;i++) {
xbins[i] = gPad->PadtoX(xlogmin+ i*dlogx);
}
fHistogram = new TH1F("Func",(char*)GetTitle(),fNpx,xbins);
fHistogram->SetBit(kLogX);
delete [] xbins;
} else {
fHistogram = new TH1F("Func",(char*)GetTitle(),fNpx,xmin,xmax);
}
if (!fHistogram) return;
fHistogram->SetDirectory(0);
}
InitArgs(xv,fParams);
for (i=1;i<=fNpx;i++) {
xv[0] = fHistogram->GetBinCenter(i);
fHistogram->SetBinContent(i,EvalPar(xv,fParams));
}
//*-*- Copy Function attributes to histogram attributes
fHistogram->SetBit(kNoStats);
fHistogram->SetMinimum(fMinimum);
fHistogram->SetMaximum(fMaximum);
fHistogram->SetLineColor(GetLineColor());
fHistogram->SetLineStyle(GetLineStyle());
fHistogram->SetLineWidth(GetLineWidth());
fHistogram->SetFillColor(GetFillColor());
fHistogram->SetFillStyle(GetFillStyle());
fHistogram->SetMarkerColor(GetMarkerColor());
fHistogram->SetMarkerStyle(GetMarkerStyle());
fHistogram->SetMarkerSize(GetMarkerSize());
//*-*- Draw the histogram
if (opt.Length() == 0) fHistogram->Paint("lf");
else if (opt == "same") fHistogram->Paint("lfsame");
else fHistogram->Paint(option);
}
//______________________________________________________________________________
void TF1::Print(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Dump this function with its attributes*-*-*-*-*-*-*-*-*-*
//*-* ==================================
TFormula::Print(option);
if (fHistogram) fHistogram->Print(option);
}
//______________________________________________________________________________
void TF1::Save(Float_t xmin, Float_t xmax)
{
// Save values of function in array fSave
if (fSave != 0) {delete [] fSave; fSave = 0;}
fNsave = fNpx;
if (fNsave <= 0) return;
fSave = new Double_t[fNsave+10];
Int_t i;
Float_t dx = (xmax-xmin)/fNsave;
if (dx <= 0) {
dx = (fXmax-fXmin)/fNsave;
fNsave--;
xmin = fXmin +0.5*dx;
xmax = fXmax -0.5*dx;
}
Double_t xv[1];
InitArgs(xv,fParams);
for (i=0;i<=fNsave;i++) {
xv[0] = xmin + dx*i;
fSave[i] = EvalPar(xv,fParams);
}
fSave[fNsave+2] = xmin;
fSave[fNsave+3] = xmax;
}
//______________________________________________________________________________
void TF1::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
char quote = '"';
out<<" "<<endl;
if (gROOT->ClassSaved(TF1::Class())) {
out<<" ";
} else {
out<<" TF1 *";
}
out<<GetName()<<" = new TF1("<<quote<<GetName()<<quote<<","<<quote<<GetTitle()<<quote<<","<<fXmin<<","<<fXmax<<");"<<endl;
if (GetFillColor() != 0) {
out<<" "<<GetName()<<"->SetFillColor("<<GetFillColor()<<");"<<endl;
}
if (GetFillStyle() != 1001) {
out<<" "<<GetName()<<"->SetFillStyle("<<GetFillStyle()<<");"<<endl;
}
if (GetMarkerColor() != 1) {
out<<" "<<GetName()<<"->SetMarkerColor("<<GetMarkerColor()<<");"<<endl;
}
if (GetMarkerStyle() != 1) {
out<<" "<<GetName()<<"->SetMarkerStyle("<<GetMarkerStyle()<<");"<<endl;
}
if (GetMarkerSize() != 1) {
out<<" "<<GetName()<<"->SetMarkerSize("<<GetMarkerSize()<<");"<<endl;
}
if (GetLineColor() != 1) {
out<<" "<<GetName()<<"->SetLineColor("<<GetLineColor()<<");"<<endl;
}
if (GetLineWidth() != 4) {
out<<" "<<GetName()<<"->SetLineWidth("<<GetLineWidth()<<");"<<endl;
}
if (GetLineStyle() != 1) {
out<<" "<<GetName()<<"->SetLineStyle("<<GetLineStyle()<<");"<<endl;
}
if (GetNpx() != 100) {
out<<" "<<GetName()<<"->SetNpx("<<GetNpx()<<");"<<endl;
}
if (GetChisquare() != 0) {
out<<" "<<GetName()<<"->SetChisquare("<<GetChisquare()<<");"<<endl;
}
Double_t parmin, parmax;
for (Int_t i=0;i<fNpar;i++) {
out<<" "<<GetName()<<"->SetParameter("<<i<<","<<GetParameter(i)<<");"<<endl;
out<<" "<<GetName()<<"->SetParError("<<i<<","<<GetParError(i)<<");"<<endl;
GetParLimits(i,parmin,parmax);
out<<" "<<GetName()<<"->SetParLimits("<<i<<","<<parmin<<","<<parmax<<");"<<endl;
}
out<<" "<<GetName()<<"->Draw("
<<quote<<option<<quote<<");"<<endl;
}
//______________________________________________________________________________
void TF1::SetNpx(Int_t npx)
{
//*-*-*-*-*-*-*-*Set the number of points used to draw the function*-*-*-*-*-*
//*-* ==================================================
if(npx > 4 && npx < 100000) fNpx = npx;
Update();
}
//______________________________________________________________________________
void TF1::SetParLimits(Int_t ipar, Double_t parmin, Double_t parmax)
{
//*-*-*-*-*-*Set limits for parameter ipar*-*-*-*
//*-* =============================
// The specified limits will be used in a fit operation
// when the option "B" is specified (Bounds).
if (ipar < 0 || ipar > fNpar-1) return;
Int_t i;
if (!fParMin) {fParMin = new Double_t[fNpar]; for (i=0;i<fNpar;i++) fParMin[i]=0;}
if (!fParMax) {fParMax = new Double_t[fNpar]; for (i=0;i<fNpar;i++) fParMin[i]=0;}
fParMin[ipar] = parmin;
fParMax[ipar] = parmax;
}
//______________________________________________________________________________
void TF1::SetRange(Float_t xmin, Float_t xmax)
{
//*-*-*-*-*-*Initialize the upper and lower bounds to draw the function*-*-*-*
//*-* ==========================================================
// The function range is also used in an histogram fit operation
// when the option "R" is specified.
fXmin = xmin;
fXmax = xmax;
Update();
}
//_______________________________________________________________________
void TF1::Streamer(TBuffer &b)
{
//*-*-*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =========================================
if (b.IsReading()) {
Version_t v = b.ReadVersion();
TFormula::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fXmin;
b >> fXmax;
b >> fNpx;
b >> fType;
b >> fChisquare;
b.ReadArray(fParErrors);
if (v > 1) {
b.ReadArray(fParMin);
b.ReadArray(fParMax);
} else {
fParMin = new Double_t[fNpar+1];
fParMax = new Double_t[fNpar+1];
}
b >> fNpfits;
if (v == 1) {
b >> fHistogram;
delete fHistogram; fHistogram = 0;
}
if (v > 1) {
b >> fMinimum;
b >> fMaximum;
}
if (v > 2) {
b >> fNsave;
if (fNsave > 0) {
fSave = new Double_t[fNsave+10];
b.ReadArray(fSave);
} else fSave = 0;
}
} else {
b.WriteVersion(TF1::IsA());
TFormula::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b << fXmin;
b << fXmax;
b << fNpx;
b << fType;
b << fChisquare;
b.WriteArray(fParErrors,fNpar);
b.WriteArray(fParMin,fNpar);
b.WriteArray(fParMax,fNpar);
b << fNpfits;
b << fMinimum;
b << fMaximum;
Int_t saved = 0;
if (fType > 0 && fNsave <= 0) { saved = 1; Save(0,0);}
b << fNsave;
if (fNsave > 0) b.WriteArray(fSave, fNsave+10);
if (saved) {delete [] fSave; fSave = 0; fNsave = 0;}
}
}
//_______________________________________________________________________
void TF1::Update()
{
// called by functions such as SetRange, SetNpx, SetParameters
// to force the deletion of the associated histogram or Integral
delete fHistogram;
fHistogram = 0;
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
}
*/
//
//
// Author(s): A.C. Genz, A.A. Malik
// converted/adaptedted by R.Brun to C++ from Fortran CERNLIB routine RADMUL (D120)
// The new code features many changes compared to the Fortran version.
// Note that this function is currently called only by TF2::Integral (n=2)
// and TF3::Integral (n=3).
//
// This function computes, to an attempted specified accuracy, the value of
// the integral over an n-dimensional rectangular region.
//
// N Number of dimensions.
// A,B One-dimensional arrays of length >= N . On entry A[i], and B[i],
// contain the lower and upper limits of integration, respectively.
// EPS Specified relative accuracy.
// RELERR Contains, on exit, an estimation of the relative accuray of RESULT.
//
// Method:
//
// An integration rule of degree seven is used together with a certain
// strategy of subdivision.
// For a more detailed description of the method see References.
//
// Notes:
//
// 1.Multi-dimensional integration is time-consuming. For each rectangular
// subregion, the routine requires function evaluations.
// Careful programming of the integrand might result in substantial saving
// of time.
// 2.Numerical integration usually works best for smooth functions.
// Some analysis or suitable transformations of the integral prior to
// numerical work may contribute to numerical efficiency.
//
// References:
//
// 1.A.C. Genz and A.A. Malik, Remarks on algorithm 006:
// An adaptive algorithm for numerical integration over
// an N-dimensional rectangular region, J. Comput. Appl. Math. 6 (1980) 295-302.
// 2.A. van Doren and L. de Ridder, An adaptive algorithm for numerical
// integration over an n-dimensional cube, J.Comput. Appl. Math. 2 (1976) 207-217.
//
//=========================================================================
Double_t ctr[15], wth[15], wthl[15], z[15];
const Double_t xl2 = 0.358568582800318073;
const Double_t xl4 = 0.948683298050513796;
const Double_t xl5 = 0.688247201611685289;
const Double_t w2 = 980./6561;
const Double_t w4 = 200./19683;
const Double_t wp2 = 245./486;
const Double_t wp4 = 25./729;
Double_t wn1[14] = { -0.193872885230909911, -0.555606360818980835,
-0.876695625666819078, -1.15714067977442459, -1.39694152314179743,
-1.59609815576893754, -1.75461057765584494, -1.87247878880251983,
-1.94970278920896201, -1.98628257887517146, -1.98221815780114818,
-1.93750952598689219, -1.85215668343240347, -1.72615963013768225};
Double_t wn3[14] = { 0.0518213686937966768, 0.0314992633236803330,
0.0111771579535639891,-0.00914494741655235473,-0.0294670527866686986,
-0.0497891581567850424,-0.0701112635269013768, -0.0904333688970177241,
-0.110755474267134071, -0.131077579637250419, -0.151399685007366752,
-0.171721790377483099, -0.192043895747599447, -0.212366001117715794};
Double_t wn5[14] = { 0.871183254585174982e-01, 0.435591627292587508e-01,
0.217795813646293754e-01, 0.108897906823146873e-01, 0.544489534115734364e-02,
0.272244767057867193e-02, 0.136122383528933596e-02, 0.680611917644667955e-03,
0.340305958822333977e-03, 0.170152979411166995e-03, 0.850764897055834977e-04,
0.425382448527917472e-04, 0.212691224263958736e-04, 0.106345612131979372e-04};
Double_t wpn1[14] = { -1.33196159122085045, -2.29218106995884763,
-3.11522633744855959, -3.80109739368998611, -4.34979423868312742,
-4.76131687242798352, -5.03566529492455417, -5.17283950617283939,
-5.17283950617283939, -5.03566529492455417, -4.76131687242798352,
-4.34979423868312742, -3.80109739368998611, -3.11522633744855959};
Double_t wpn3[14] = { 0.0445816186556927292, -0.0240054869684499309,
-0.0925925925925925875, -0.161179698216735251, -0.229766803840877915,
-0.298353909465020564, -0.366941015089163228, -0.435528120713305891,
-0.504115226337448555, -0.572702331961591218, -0.641289437585733882,
-0.709876543209876532, -0.778463648834019195, -0.847050754458161859};
Double_t result = 0;
Double_t abserr = 0;
Int_t ifail = 3;
if (n < 2 || n > 15) return 0;
Double_t twondm = TMath::Power(2,n);
Int_t ifncls = 0;
Bool_t ldv = kFALSE;
Int_t irgnst = 2*n+3;
Int_t irlcls = Int_t(twondm) +2*n*(n+1)+1;
Int_t isbrgn = irgnst;
Int_t isbrgs = irgnst;
// The original algorithm expected a parameter MAXPTS
// where MAXPTS = Maximum number of function evaluations to be allowed.
// Here we set MAXPTS to 2*(the lowest possible value)
Int_t maxpts = 2*irlcls;
Int_t minpts = 1;
// The original agorithm expected a working space array WK of length IWK
// with IWK Length ( >= (2N + 3) * (1 + MAXPTS/(2**N + 2N(N + 1) + 1))/2).
// Here, this array is allocated dynamically
Int_t iwk = irgnst*(1 +maxpts/irlcls)/2;
Double_t *wk = new Double_t[iwk+10];
Int_t j;
for (j=0;j<n;j++) {
ctr[j] = (b[j] + a[j])*0.5;
wth[j] = (b[j] - a[j])*0.5;
}
Double_t rgnvol, sum1, sum2, sum3, sum4, sum5, difmax, f2, f3, dif;
Double_t rgncmp=0, rgnval, rgnerr;
Int_t j1, k, l, m, idvaxn=0, idvax0=0, isbtmp, isbtpp;
InitArgs(z,fParams);
L20:
rgnvol = twondm;
for (j=0;j<n;j++) {
rgnvol *= wth[j];
z[j] = ctr[j];
}
sum1 = EvalPar(z,fParams); //evaluate function
difmax = 0;
sum2 = 0;
sum3 = 0;
for (j=0;j<n;j++) {
z[j] = ctr[j] - xl2*wth[j];
f2 = EvalPar(z,fParams);
z[j] = ctr[j] + xl2*wth[j];
f2 += EvalPar(z,fParams);
wthl[j] = xl4*wth[j];
z[j] = ctr[j] - wthl[j];
f3 = EvalPar(z,fParams);
z[j] = ctr[j] + wthl[j];
f3 += EvalPar(z,fParams);
sum2 += f2;
sum3 += f3;
dif = TMath::Abs(7*f2-f3-12*sum1);
difmax = TMath::Max(dif, difmax);
if (difmax == dif) idvaxn = j+1;
z[j] = ctr[j];
}
sum4 = 0;
for (j=1;j<n;j++) {
j1 = j-1;
for (k=j;k<n;k++) {
for (l=0;l<2;l++) {
wthl[j1] = -wthl[j1];
z[j1] = ctr[j1] + wthl[j1];
for (m=0;m<2;m++) {
wthl[k] = -wthl[k];
z[k] = ctr[k] + wthl[k];
sum4 += EvalPar(z,fParams);
}
}
z[k] = ctr[k];
}
z[j1] = ctr[j1];
}
sum5 = 0;
for (j=0;j<n;j++) {
wthl[j] = -xl5*wth[j];
z[j] = ctr[j] + wthl[j];
}
L90:
sum5 += EvalPar(z,fParams);
for (j=0;j<n;j++) {
wthl[j] = -wthl[j];
z[j] = ctr[j] + wthl[j];
if (wthl[j] > 0) goto L90;
}
rgncmp = rgnvol*(wpn1[n-2]*sum1+wp2*sum2+wpn3[n-2]*sum3+wp4*sum4);
rgnval = wn1[n-2]*sum1+w2*sum2+wn3[n-2]*sum3+w4*sum4+wn5[n-2]*sum5;
rgnval *= rgnvol;
rgnerr = TMath::Abs(rgnval-rgncmp);
result += rgnval;
abserr += rgnerr;
ifncls += irlcls;
if (ldv) {
L110:
isbtmp = 2*isbrgn;
if (isbtmp > isbrgs) goto L160;
if (isbtmp < isbrgs) {
isbtpp = isbtmp + irgnst;
if (wk[isbtmp-1] < wk[isbtpp-1]) isbtmp = isbtpp;
}
if (rgnerr >= wk[isbtmp-1]) goto L160;
for (k=0;k<irgnst;k++) {
wk[isbrgn-k-1] = wk[isbtmp-k-1];
}
isbrgn = isbtmp;
goto L110;
}
L140:
isbtmp = (isbrgn/(2*irgnst))*irgnst;
if (isbtmp >= irgnst && rgnerr > wk[isbtmp-1]) {
for (k=0;k<irgnst;k++) {
wk[isbrgn-k-1] = wk[isbtmp-k-1];
}
isbrgn = isbtmp;
goto L140;
}
L160:
wk[isbrgn-1] = rgnerr;
wk[isbrgn-2] = rgnval;
wk[isbrgn-3] = Double_t(idvaxn);
for (j=0;j<n;j++) {
isbtmp = isbrgn-2*j-4;
wk[isbtmp] = ctr[j];
wk[isbtmp-1] = wth[j];
}
if (ldv) {
ldv = kFALSE;
ctr[idvax0-1] += 2*wth[idvax0-1];
isbrgs += irgnst;
isbrgn = isbrgs;
goto L20;
}
relerr = abserr/TMath::Abs(result);
if (isbrgs+irgnst > iwk) ifail = 2;
if (ifncls+2*irlcls > maxpts) ifail = 1;
if (relerr < eps && ifncls >= minpts) ifail = 0;
if (ifail == 3) {
ldv = kTRUE;
isbrgn = irgnst;
abserr -= wk[isbrgn-1];
result -= wk[isbrgn-2];
idvax0 = Int_t(wk[isbrgn-3]);
for (j=0;j<n;j++) {
isbtmp = isbrgn-2*j-4;
ctr[j] = wk[isbtmp];
wth[j] = wk[isbtmp-1];
}
wth[idvax0-1] = 0.5*wth[idvax0-1];
ctr[idvax0-1] -= wth[idvax0-1];
goto L20;
}
// IFAIL On exit:
// 0 Normal exit. . At most MAXPTS calls to the function F were performed.
// 1 MAXPTS is too small for the specified accuracy EPS. RESULT and RELERR
// contain the values obtainable for the specified value of MAXPTS.
//
delete [] wk;
// Int_t nfnevl = ifncls; //number of function evaluations performed.
return result; //an approximate value of the integral
}
//______________________________________________________________________________
void TF1::Paint(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Paint this function with its current attributes*-*-*-*-*
//*-* ===============================================
const Int_t kLogX = BIT(15);
Int_t i;
Double_t xv[1];
TString opt = option;
opt.ToLower();
Float_t xmin, xmax, pmin, pmax;
pmin = gPad->PadtoX(gPad->GetUxmin());
pmax = gPad->PadtoX(gPad->GetUxmax());
xmin = fXmin;
xmax = fXmax;
if (opt.Contains("same")) {
if (xmax < pmin) return; // Otto: completely outside
if (xmin > pmax) return;
if (xmin < pmin) xmin = pmin;
if (xmax > pmax) xmax = pmax;
} else {
gPad->Clear();
}
//*-*- Create a temporary histogram and fill each channel with the function value
if (fHistogram) {
if (!gPad->GetLogx() && fHistogram->TestBit(kLogX)) { delete fHistogram; fHistogram = 0;}
if ( gPad->GetLogx() && !fHistogram->TestBit(kLogX)) { delete fHistogram; fHistogram = 0;}
}
if (fHistogram) {
if (xmin != fXmin || xmax != fXmax) fHistogram->GetXaxis()->SetLimits(xmin,xmax);
} else {
// if logx, we must bin in logx and not in x !!!
// otherwise if several decades, one gets crazy results
if (xmin > 0 && gPad->GetLogx()) {
Float_t *xbins = new Float_t[fNpx+1];
Float_t xlogmin = TMath::Log10(xmin);
Float_t xlogmax = TMath::Log10(xmax);
Float_t dlogx = (xlogmax-xlogmin)/((Float_t)fNpx);
for (i=0;i<=fNpx;i++) {
xbins[i] = gPad->PadtoX(xlogmin+ i*dlogx);
}
fHistogram = new TH1F("Func",(char*)GetTitle(),fNpx,xbins);
fHistogram->SetBit(kLogX);
delete [] xbins;
} else {
fHistogram = new TH1F("Func",(char*)GetTitle(),fNpx,xmin,xmax);
}
if (!fHistogram) return;
fHistogram->SetDirectory(0);
}
InitArgs(xv,fParams);
for (i=1;i<=fNpx;i++) {
xv[0] = fHistogram->GetBinCenter(i);
fHistogram->SetBinContent(i,EvalPar(xv,fParams));
}
//*-*- Copy Function attributes to histogram attributes
fHistogram->SetBit(kNoStats);
fHistogram->SetMinimum(fMinimum);
fHistogram->SetMaximum(fMaximum);
fHistogram->SetLineColor(GetLineColor());
fHistogram->SetLineStyle(GetLineStyle());
fHistogram->SetLineWidth(GetLineWidth());
fHistogram->SetFillColor(GetFillColor());
fHistogram->SetFillStyle(GetFillStyle());
fHistogram->SetMarkerColor(GetMarkerColor());
fHistogram->SetMarkerStyle(GetMarkerStyle());
fHistogram->SetMarkerSize(GetMarkerSize());
//*-*- Draw the histogram
if (opt.Length() == 0) fHistogram->Paint("lf");
else if (opt == "same") fHistogram->Paint("lfsame");
else fHistogram->Paint(option);
}
//______________________________________________________________________________
void TF1::Print(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Dump this function with its attributes*-*-*-*-*-*-*-*-*-*
//*-* ==================================
TFormula::Print(option);
if (fHistogram) fHistogram->Print(option);
}
//______________________________________________________________________________
void TF1::Save(Float_t xmin, Float_t xmax)
{
// Save values of function in array fSave
if (fSave != 0) {delete [] fSave; fSave = 0;}
fNsave = fNpx;
if (fNsave <= 0) return;
fSave = new Double_t[fNsave+10];
Int_t i;
Float_t dx = (xmax-xmin)/fNsave;
if (dx <= 0) {
dx = (fXmax-fXmin)/fNsave;
fNsave--;
xmin = fXmin +0.5*dx;
xmax = fXmax -0.5*dx;
}
Double_t xv[1];
InitArgs(xv,fParams);
for (i=0;i<=fNsave;i++) {
xv[0] = xmin + dx*i;
fSave[i] = EvalPar(xv,fParams);
}
fSave[fNsave+2] = xmin;
fSave[fNsave+3] = xmax;
}
//______________________________________________________________________________
void TF1::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
char quote = '"';
out<<" "<<endl;
if (gROOT->ClassSaved(TF1::Class())) {
out<<" ";
} else {
out<<" TF1 *";
}
out<<GetName()<<" = new TF1("<<quote<<GetName()<<quote<<","<<quote<<GetTitle()<<quote<<","<<fXmin<<","<<fXmax<<");"<<endl;
if (GetFillColor() != 0) {
out<<" "<<GetName()<<"->SetFillColor("<<GetFillColor()<<");"<<endl;
}
if (GetFillStyle() != 1001) {
out<<" "<<GetName()<<"->SetFillStyle("<<GetFillStyle()<<");"<<endl;
}
if (GetMarkerColor() != 1) {
out<<" "<<GetName()<<"->SetMarkerColor("<<GetMarkerColor()<<");"<<endl;
}
if (GetMarkerStyle() != 1) {
out<<" "<<GetName()<<"->SetMarkerStyle("<<GetMarkerStyle()<<");"<<endl;
}
if (GetMarkerSize() != 1) {
out<<" "<<GetName()<<"->SetMarkerSize("<<GetMarkerSize()<<");"<<endl;
}
if (GetLineColor() != 1) {
out<<" "<<GetName()<<"->SetLineColor("<<GetLineColor()<<");"<<endl;
}
if (GetLineWidth() != 4) {
out<<" "<<GetName()<<"->SetLineWidth("<<GetLineWidth()<<");"<<endl;
}
if (GetLineStyle() != 1) {
out<<" "<<GetName()<<"->SetLineStyle("<<GetLineStyle()<<");"<<endl;
}
if (GetNpx() != 100) {
out<<" "<<GetName()<<"->SetNpx("<<GetNpx()<<");"<<endl;
}
if (GetChisquare() != 0) {
out<<" "<<GetName()<<"->SetChisquare("<<GetChisquare()<<");"<<endl;
}
Double_t parmin, parmax;
for (Int_t i=0;i<fNpar;i++) {
out<<" "<<GetName()<<"->SetParameter("<<i<<","<<GetParameter(i)<<");"<<endl;
out<<" "<<GetName()<<"->SetParError("<<i<<","<<GetParError(i)<<");"<<endl;
GetParLimits(i,parmin,parmax);
out<<" "<<GetName()<<"->SetParLimits("<<i<<","<<parmin<<","<<parmax<<");"<<endl;
}
out<<" "<<GetName()<<"->Draw("
<<quote<<option<<quote<<");"<<endl;
}
//______________________________________________________________________________
void TF1::SetNpx(Int_t npx)
{
//*-*-*-*-*-*-*-*Set the number of points used to draw the function*-*-*-*-*-*
//*-* ==================================================
if(npx > 4 && npx < 100000) fNpx = npx;
Update();
}
//______________________________________________________________________________
void TF1::SetParLimits(Int_t ipar, Double_t parmin, Double_t parmax)
{
//*-*-*-*-*-*Set limits for parameter ipar*-*-*-*
//*-* =============================
// The specified limits will be used in a fit operation
// when the option "B" is specified (Bounds).
if (ipar < 0 || ipar > fNpar-1) return;
Int_t i;
if (!fParMin) {fParMin = new Double_t[fNpar]; for (i=0;i<fNpar;i++) fParMin[i]=0;}
if (!fParMax) {fParMax = new Double_t[fNpar]; for (i=0;i<fNpar;i++) fParMin[i]=0;}
fParMin[ipar] = parmin;
fParMax[ipar] = parmax;
}
//______________________________________________________________________________
void TF1::SetRange(Float_t xmin, Float_t xmax)
{
//*-*-*-*-*-*Initialize the upper and lower bounds to draw the function*-*-*-*
//*-* ==========================================================
// The function range is also used in an histogram fit operation
// when the option "R" is specified.
fXmin = xmin;
fXmax = xmax;
Update();
}
//_______________________________________________________________________
void TF1::Streamer(TBuffer &b)
{
//*-*-*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =========================================
if (b.IsReading()) {
Version_t v = b.ReadVersion();
TFormula::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fXmin;
b >> fXmax;
b >> fNpx;
b >> fType;
b >> fChisquare;
b.ReadArray(fParErrors);
if (v > 1) {
b.ReadArray(fParMin);
b.ReadArray(fParMax);
} else {
fParMin = new Double_t[fNpar+1];
fParMax = new Double_t[fNpar+1];
}
b >> fNpfits;
if (v == 1) {
b >> fHistogram;
delete fHistogram; fHistogram = 0;
}
if (v > 1) {
b >> fMinimum;
b >> fMaximum;
}
if (v > 2) {
b >> fNsave;
if (fNsave > 0) {
fSave = new Double_t[fNsave+10];
b.ReadArray(fSave);
} else fSave = 0;
}
} else {
b.WriteVersion(TF1::IsA());
TFormula::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b << fXmin;
b << fXmax;
b << fNpx;
b << fType;
b << fChisquare;
b.WriteArray(fParErrors,fNpar);
b.WriteArray(fParMin,fNpar);
b.WriteArray(fParMax,fNpar);
b << fNpfits;
b << fMinimum;
b << fMaximum;
Int_t saved = 0;
if (fType > 0 && fNsave <= 0) { saved = 1; Save(0,0);}
b << fNsave;
if (fNsave > 0) b.WriteArray(fSave, fNsave+10);
if (saved) {delete [] fSave; fSave = 0; fNsave = 0;}
}
}
//_______________________________________________________________________
void TF1::Update()
{
// called by functions such as SetRange, SetNpx, SetParameters
// to force the deletion of the associated histogram or Integral
delete fHistogram;
fHistogram = 0;
if (fIntegral) {delete [] fIntegral; fIntegral = 0;}
}