|
5. Справедливость и оптимальность экономических алгоритмов
управления потоками.
Сформулируем четыре критерия справедливости распределения ресурсов между виртуальными каналами.
(F1) Распределение {X1, X2, ..., XN} справедливо, если для всех a из A выполняется неравенство T(Xa)>0.
Этот критерий утверждает, что не должно быть виртуальных каналов, которым досталась бы в результате распределения нулевая пропускная способность.
Будем называть реальный канал i из La заторным каналом (от слова затор, узкое место) виртуального канала a, если T(Xa)=xia. Таким образом, заторный канал определяет пропускную способность виртуального канала.
(F2) Пусть i является заторным каналом виртуального канала a. Распределение {X1, X2, ..., XN} справедливо, если xia>=xib для всех b из A.
Это условие иногда называют максиминным, поскольку оно определяется исходя из максимизации минимума пропускной способности. Данный критерий предполагает, что все виртуальные каналы стремятся максимизировать пропускную способность, но не учитывают задержку.
(F3) Распределение {X1, X2, ..., XN} справедливо, если для всех a из A Xa&aY для всех Y из Ba(P).
Это условие построено на основе понятия устойчивости по Нэшу (из теории игр). В отличие от F1 и F2, критерий F3 учитывает и пропускную способность, и задержку (в силу того, что он основывается на отношении предпочтения).
Прежде чем сформулировать четвертый критерий, введем несколько вспомогательных понятий.
Назовем коалицией S некоторую подсистему A. Коалиция S может улучшить распределение {X1, X2, ..., XN}, если найдет другое распределение {Y1, Y2, ..., YN} такое, что:
- Ya=Xa, где a не принадлежит S (формирование коалиции не влияет на тех, кто в нее не входит);
- Ya&aXa, для a из S ( для всех членов коалиции новое распределение не хуже старого);
- найдется такое a из S, для которого Ya&saXa (хотя бы для одного члена коалиции новое распределение строго лучше старого).
Теперь определим четвертый критерий.
(F4) Распределение {X1, X2, ..., XN} справедливо, если нет таких коалиций, которые могли бы улучшить распределение.
Условие F4 эквивалентно определению оптимальности по Парето .
Очевидно, что справедливы утверждения:
- Если F2, то F1;
- Если F4, то F3.
Следующая лемма показывает, что "экономика компьютерной сети" распределяет ресурсы справедливо с точки зрения критериев F1 и F3.
Лемма 2.
Пусть P - вектор цен, фa(P) - вектор спроса виртуального канала a при ценах P, X - вектор ресурсов, такой что X не равен фa(P). Тогда:
- ф a(P)*P=Wa
- Если X&aфa(P), то X*P>= фa(P)*P
- Если X&sa фa(P), то X*P> фa(P)*P
Доказательство.
В случае, если T(фa(P))<ga, утверждения леммы очевидны. Пусть T(фa(P))>=ga.
(1) Если фa(P)*P<Wa, у виртуального канала образуется остаток q=Wa-фa(P)*P, где q>0. Приобретение q/pi полосы пропускания реального канала связи i из La позволяет уменьшить задержку, ибо она (задержка) является монотонно убывающей функцией от xi, при xi>=ga. Это значит, что фa(P) - неоптимальный вектор. Полученное противоречие доказывает первое утверждение леммы.
(2,3) Допустим противоположное: если X&a фa(P), то X*P< фa(P)*P.
Обозначим:
- ui= фia-ga, если i из La.
ui= фia, если i не принадлежит La.
- hi=xi-ga, при i из La.
hi=xi, если i не принадлежит La.
- U=(u1,u2,...,um(a)), H=(h1,h2,...,hm(a)).
Тогда, P*H<=Wa-Qa*ga и H -допустимо.
Если X равноценно фa(P) для a, то F(U)=F(H). Но это противоречит строгой выпуклости функции F.
Если X&as фa(P), то F(H)<F(U). Приходим к противоречию с оптимальностью U(определением фa(P)). Это завершает доказательство леммы .
Согласно определению, цены P и бюджет Wa принимают только положительные значения. На основании этого и в силу утверждения части 1 леммы 2 распределение фa(P) является справедливым с т.зр. критерия F1. Справедливость с т.зр. критерия F3 вытекает из утверждений пунктов 2 и 3 леммы 2.
Воспользуемся леммой 2 для доказательства следующей теоремы, устанавливающей парето-оптимальность распределения в "экономике компьютерной сети" .
Теорема 1.
Пусть P - вектор равновесных цен. Тогда распределение {ф1(P), ф2(P),..., фN(P)} является парето-оптимальным и единственным.
Доказательство.
Единственность. В главе 3 было показано, что система спроса Фa(P) содержит один единственный элемент (для всех a из A). Следовательно и вектор {ф1(P), ф2(P),..., фN(P)} - единственный.
Парето-оптимальность. Допустим, что коалиция S={1,2,...,s} сформировала новое распределение ф', такое что:
- фi'(P)&i фi(P), для всех i из S.
- фj'(P)&siфj(P), хотя бы для одного j из S.
Следовательно, согласно лемме 2:
- фi'(P)*P>= фi(P)*P, для всех i из S.
- фj'(P)*P> фj(P)*P, хотя бы для одного j из S.
Значит,
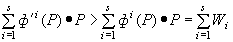 (13) (13)
Это свидетельствует о том, что коалиция не может улучшить распределение. В силу формулировки F4, распределение {ф1(P), ф2(P),..., фN(P)} - оптимально по Парето. Теорема доказана .
|