//*CMZ : 2.22/10 27/07/99 17.07.51 by Rene Brun
//*CMZ : 2.22/09 12/07/99 17.47.57 by Rene Brun
//*CMZ : 2.22/07 05/07/99 16.41.12 by Rene Brun
//*CMZ : 2.22/05 15/06/99 16.20.19 by Rene Brun
//*CMZ : 2.22/02 26/05/99 12.35.40 by Rene Brun
//*CMZ : 2.22/00 17/05/99 08.50.46 by Rene Brun
//*CMZ : 2.21/07 02/03/99 17.04.25 by Rene Brun
//*CMZ : 2.21/06 15/02/99 09.00.59 by Rene Brun
//*CMZ : 2.21/03 22/01/99 08.42.02 by Rene Brun
//*CMZ : 2.21/02 18/01/99 13.51.25 by Rene Brun
//*CMZ : 2.21/01 11/01/99 08.34.24 by Rene Brun
//*CMZ : 2.20/06 17/12/98 09.41.02 by Rene Brun
//*CMZ : 2.20/05 15/12/98 09.17.20 by Rene Brun
//*CMZ : 2.20/00 01/12/98 09.22.49 by Rene Brun
//*CMZ : 2.00/13 20/10/98 16.41.59 by Rene Brun
//*CMZ : 2.00/12 01/10/98 09.10.09 by Rene Brun
//*CMZ : 2.00/06 15/09/98 02.06.32 by Rene Brun
//*CMZ : 2.00/05 08/04/98 12.34.10 by Rene Brun
//*CMZ : 2.00/04 06/04/98 13.29.37 by Rene Brun
//*CMZ : 2.00/02 16/03/98 09.36.40 by Rene Brun
//*CMZ : 2.00/00 05/03/98 18.02.39 by Fons Rademakers
//*CMZ : 1.03/09 15/12/97 09.17.18 by Rene Brun
//*-- Author : Rene Brun, Olivier Couet 12/12/94
//*KEEP,CopyRight,T=C.
/*************************************************************************
* Copyright(c) 1995-1999, The ROOT System, All rights reserved. *
* Authors: Rene Brun, Fons Rademakers. *
* For list of contributors see $ROOTSYS/AA_CREDITS. *
* *
* Permission to use, copy, modify and distribute this software and its *
* documentation for non-commercial purposes is hereby granted without *
* fee, provided that the above copyright notice appears in all copies *
* and that both the copyright notice and this permission notice appear *
* in the supporting documentation. The authors make no claims about the *
* suitability of this software for any purpose. It is provided "as is" *
* without express or implied warranty. *
*************************************************************************/
//*KEND.
#include <string.h>
#include <fstream.h>
//*KEEP,TROOT.
#include "TROOT.h"
//*KEEP,TGraph.
#include "TGraph.h"
//*KEEP,TGaxis.
#include "TGaxis.h"
//*KEEP,TH1.
#include "TH1.h"
//*KEEP,TLine.
#include "TLine.h"
//*KEEP,TText.
#include "TText.h"
//*KEEP,TStyle.
#include "TStyle.h"
//*KEEP,TMath.
#include "TMath.h"
//*KEEP,Foption.
#include "Foption.h"
//*KEEP,TMinuit.
#include "TMinuit.h"
//*KEEP,TVirtualPad.
#include "TVirtualPad.h"
//*KEEP,TInterpreter, T=C++.
#include "TInterpreter.h"
//*KEND.
const Int_t NPMAX = 204;
const Int_t kNoStats = BIT(9);
const Int_t kClipFrame = BIT(10);
const Int_t kFitInit = BIT(19);
static Float_t xwork[NPMAX];
static Float_t ywork[NPMAX];
static Float_t xworkl[NPMAX];
static Float_t yworkl[NPMAX];
R__EXTERN TH1 *gCurrentHist;
R__EXTERN TF1 *gF1;
R__EXTERN Foption_t Foption;
static Int_t xfirst,xlast;
static Float_t xmin, xmax, ymin, ymax;
extern void GraphFitChisquare(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
extern void H1LeastSquareSeqnd(Int_t n, Double_t *a, Int_t idim, Int_t &ifail, Int_t k, Double_t *b);
ClassImp(TGraph)
//______________________________________________________________________________
//
// A Graph is a graphics object made of two arrays X and Y
// with npoints each.
// This class supports essentially two graph categories:
// - General case with non equidistant points
// - Special case with equidistant points
// The various format options to draw a Graph are explained in
// TGraph::PaintGraph and TGraph::PaintGrapHist
// These two functions are derived from the HIGZ routines IGRAPH and IGHIST
// and many modifications.
//
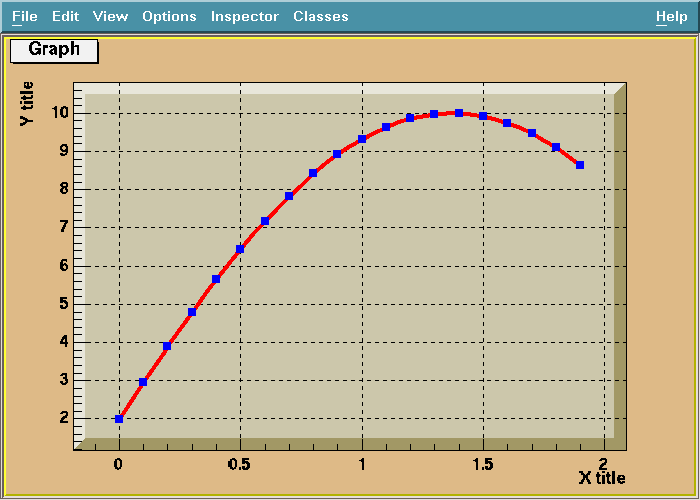
// The picture below has been generated by the following macro:
//------------------------------------------------------------------
//{
// TCanvas *c1 = new TCanvas("c1","A Simple Graph Example",200,10,700,500);
// Float_t x[100], y[100];
// Int_t n = 20;
// for (Int_t i=0;i<n;i++) {
// x[i] = i*0.1;
// y[i] = 10*sin(x[i]+0.2);
// }
// gr = new TGraph(n,x,y);
// gr->Draw("AC*");
//}
//
/*
 */
//
//
//______________________________________________________________________________
TGraph::TGraph(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =========================
fNpoints = 0;
fX = 0;
fY = 0;
fFunctions = 0;
fHistogram = 0;
fMaximum = -1111;
fMinimum = -1111;
}
//______________________________________________________________________________
TGraph::TGraph(Int_t n, Float_t *x, Float_t *y)
: TNamed("Graph","Graph"), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph normal constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
if (n <= 0) {
Error("TGraph", "illegal number of points (%d)", n);
return;
}
fFunctions = new TList(this);
fHistogram = 0;
fNpoints = n;
fX = new Float_t[n];
fY = new Float_t[n];
fMaximum = -1111;
fMinimum = -1111;
if (!x || !y) return;
for (Int_t i=0;i<n;i++) {
fX[i] = x[i];
fY[i] = y[i];
}
SetBit(kClipFrame);
}
//______________________________________________________________________________
TGraph::~TGraph()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default destructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =======================
delete [] fX;
delete [] fY;
if (!fFunctions) return;
fFunctions->Delete();
delete fFunctions;
fFunctions = 0;
delete fHistogram;
fHistogram = 0;
}
//______________________________________________________________________________
void TGraph::ComputeRange(Float_t &, Float_t &, Float_t &, Float_t &)
{
// this function is dummy in TGraph, but redefined by TGraphErrors
}
//______________________________________________________________________________
void TGraph::Draw(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ==========================================
//
// Options to draw a graph are described in TGraph::PaintGraph
char chopt[8] = " ";
if (strlen(option) < 7) strcpy(chopt,option);
else strncpy(chopt,option,7);
// in case of option *, set marker style to 3 (star) and replace
// * option by option P.
char *cstar = strchr(chopt,'*');
if (cstar) {
SetMarkerStyle(3);
cstar[0] = 'P';
}
AppendPad(chopt);
}
//______________________________________________________________________________
Int_t TGraph::DistancetoPrimitive(Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a graph*-*-*-*-*-*
//*-* ===========================================
// Compute the closest distance of approach from point px,py to this line.
// The distance is computed in pixels units.
//
//*-*- Are we on the axis?
Int_t distance;
if (fHistogram) {
distance = fHistogram->DistancetoPrimitive(px,py);
if (distance <= 0) return distance;
}
//*-*- Somewhere on the graph points?
const Int_t big = 9999;
const Int_t kMaxDiff = 10;
Int_t puxmin = gPad->XtoAbsPixel(gPad->GetUxmin());
Int_t puymin = gPad->YtoAbsPixel(gPad->GetUymin());
Int_t puxmax = gPad->XtoAbsPixel(gPad->GetUxmax());
Int_t puymax = gPad->YtoAbsPixel(gPad->GetUymax());
//*-*- return if point is not in the histogram area
if (px <= puxmin) return big;
if (py >= puymin) return big;
if (px >= puxmax) return big;
if (py <= puymax) return big;
//*-*- check if point is near one of the graph points
Int_t i, pxp, pyp, d;
distance = big;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < distance) distance = d;
}
if (distance < kMaxDiff) return distance;
for (i=0;i<fNpoints-1;i++) {
d = DistancetoLine(px, py, gPad->XtoPad(fX[i]), gPad->YtoPad(fY[i]), gPad->XtoPad(fX[i+1]), gPad->YtoPad(fY[i+1]));
if (d < distance) distance = d;
}
//*-*- Loop on the list of associated functions and user objects
TObject *f;
TIter next(fFunctions);
while ((f = (TObject*) next())) {
Int_t dist = f->DistancetoPrimitive(px,py);
if (dist < kMaxDiff) {gPad->SetSelected(f); return dist;}
}
return distance;
}
//______________________________________________________________________________
void TGraph::DrawGraph(Int_t n, Float_t *x, Float_t *y, Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with new attributes*-*-*-*-*-*-*-*-*-*
//*-* ===================================
TGraph *newgraph = new TGraph(n, x, y);
TAttLine::Copy(*newgraph);
TAttFill::Copy(*newgraph);
TAttMarker::Copy(*newgraph);
newgraph->SetBit(kCanDelete);
newgraph->AppendPad(option);
}
//______________________________________________________________________________
void TGraph::DrawPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph drawing options*-*-*-*-*-*
//*-* ==============================================
//
printf("TGraph::DrawPanel: not yet implementedn");
}
//______________________________________________________________________________
void TGraph::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
//*-* =========================================
// This member function is called when a graph is clicked with the locator
//
// If Left button clicked on one of the line end points, this point
// follows the cursor until button is released.
//
// if Middle button clicked, the line is moved parallel to itself
// until the button is released.
//
Int_t i, d;
Float_t xmin, xmax, ymin, ymax, dx, dy, dxr, dyr;
const Int_t kMaxDiff = 10;
static Bool_t MIDDLE;
static Int_t ipoint, pxp, pyp;
static Int_t px1,px2,py1,py2;
static Int_t pxold, pyold, px1old, py1old, px2old, py2old;
static Int_t dpx, dpy;
static Int_t *x=0, *y=0;
switch (event) {
case kButton1Down:
gGXW->SetLineColor(-1);
TAttLine::Modify(); //Change line attributes only if necessary
px1 = gPad->XtoAbsPixel(gPad->GetX1());
py1 = gPad->YtoAbsPixel(gPad->GetY1());
px2 = gPad->XtoAbsPixel(gPad->GetX2());
py2 = gPad->YtoAbsPixel(gPad->GetY2());
ipoint = -1;
if (x || y) break;
x = new Int_t[fNpoints+1];
y = new Int_t[fNpoints+1];
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
x[i] = pxp;
y[i] = pyp;
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) ipoint =i;
}
dpx = 0;
dpy = 0;
pxold = px;
pyold = py;
if (ipoint < 0) return;
if (ipoint == 0) {
px1old = 0;
py1old = 0;
px2old = gPad->XtoAbsPixel(fX[1]);
py2old = gPad->YtoAbsPixel(fY[1]);
} else if (ipoint == fNpoints-1) {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[fNpoints-2]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[fNpoints-2]));
px2old = 0;
py2old = 0;
} else {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint-1]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint-1]));
px2old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint+1]));
py2old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint+1]));
}
pxold = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint]));
pyold = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint]));
break;
case kMouseMotion:
MIDDLE = kTRUE;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) MIDDLE = kFALSE;
}
//*-*- check if point is close to an axis
if (MIDDLE) gPad->SetCursor(kMove);
else gPad->SetCursor(kHand);
break;
case kButton1Motion:
if (MIDDLE) {
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
dpx += px - pxold;
dpy += py - pyold;
pxold = px;
pyold = py;
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
} else {
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
pxold = px;
pxold = TMath::Max(pxold, px1);
pxold = TMath::Min(pxold, px2);
pyold = py;
pyold = TMath::Max(pyold, py2);
pyold = TMath::Min(pyold, py1);
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
}
break;
case kButton1Up:
//*-*- Compute x,y range
xmin = gPad->GetUxmin();
xmax = gPad->GetUxmax();
ymin = gPad->GetUymin();
ymax = gPad->GetUymax();
dx = xmax-xmin;
dy = ymax-ymin;
dxr = dx/(1 - gPad->GetLeftMargin() - gPad->GetRightMargin());
dyr = dy/(1 - gPad->GetBottomMargin() - gPad->GetTopMargin());
// Range() could change the size of the pad pixmap and therefore should
// be called before the other paint routines
gPad->Range(xmin - dxr*gPad->GetLeftMargin(),
ymin - dyr*gPad->GetBottomMargin(),
xmax + dxr*gPad->GetRightMargin(),
ymax + dyr*gPad->GetTopMargin());
gPad->RangeAxis(xmin, ymin, xmax, ymax);
if (MIDDLE) {
for(i=0;i<fNpoints;i++) {
fX[i] = gPad->PadtoX(gPad->AbsPixeltoX(x[i]+dpx));
fY[i] = gPad->PadtoY(gPad->AbsPixeltoY(y[i]+dpy));
}
} else {
fX[ipoint] = gPad->PadtoX(gPad->AbsPixeltoX(pxold));
fY[ipoint] = gPad->PadtoY(gPad->AbsPixeltoY(pyold));
}
delete [] x; x = 0;
delete [] y; y = 0;
gPad->Modified(kTRUE);
gGXW->SetLineColor(-1);
}
}
//______________________________________________________________________________
void TGraph::Fit(Text_t *fname, Option_t *option, Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Fit this graph with function fname*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// fname is the name of an already predefined function created by TF1
// Predefined functions such as Gaus, Expo and Poln are automatically
// created by ROOT.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TGraph::Paint for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your graph
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// graph->Fit("f1","R");
//
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,0.1,-8,100);
// func->SetParLimits(4,-10,-4);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->3 can vary freely
// Parameter 4 has boundaries [-10,-4] with initial value -8
// Parameter 5 is fixed to 100.
//
Int_t i, ierf, npar,nvpar,nparx,icstat;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,edm,errdef,werr;
TF1 *fnew1;
Double_t *arglist = new Double_t[100];
// Decode string choptin and fill Foption structure
Foption.Quiet = 0;
Foption.Verbose = 0;
Foption.Bound = 0;
Foption.Like = 0;
Foption.W1 = 0;
Foption.Errors = 0;
Foption.Range = 0;
Foption.Gradient= 0;
Foption.Nograph = 0;
Foption.Nostore = 0;
Foption.Plus = 0;
TString opt = option;
opt.ToUpper();
if (opt.Contains("Q")) Foption.Quiet = 1;
if (opt.Contains("V")){Foption.Verbose = 1; Foption.Quiet = 0;}
if (opt.Contains("W")) Foption.W1 = 1;
if (opt.Contains("E")) Foption.Errors = 1;
if (opt.Contains("R")) Foption.Range = 1;
if (opt.Contains("N")) Foption.Nostore = 1;
if (opt.Contains("0")) Foption.Nograph = 1;
if (opt.Contains("+")) Foption.Plus = 1;
xmin = fX[0];
xmax = fX[fNpoints-1];
ymin = fY[0];
ymax = fY[fNpoints-1];
for (i=0;i<fNpoints;i++) {
if (fX[i] < xmin) xmin = fX[i];
if (fX[i] > xmax) xmax = fX[i];
if (fY[i] < ymin) ymin = fY[i];
if (fY[i] > ymax) ymax = fY[i];
}
//*-*- Check if Minuit is initialized and create special functions
if (!gMinuit) gMinuit = new TMinuit(25);
if (!gROOT->GetFunction("gaus")) {
gF1 = new TF1("gaus","gaus",xmin,xmax);
gF1 = new TF1("expo","expo",xmin,xmax);
for (i=0;i<10;i++) gF1 = new TF1(Form("pol%d",i),Form("pol%d",i),xmin,xmax);
}
gMinuit->mncler();
gMinuit->SetObjectFit(this);
//*-*- Get pointer to the function by searching in the list of functions in ROOT
gF1 = gROOT->GetFunction(fname);
if (!gF1) { Printf("Unknown function: %s",fname); return; }
npar = gF1->GetNpar();
if (npar <=0) { Printf("Illegal number of parameters = %d",npar); return; }
//*-*- Check that function has same dimension as histogram
if (gF1->GetNdim() > 1) {
Printf("Error function %s is not 1-D",fname); return; }
//*-*- Is a Fit range specified?
if (Foption.Range) {
gF1->GetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
} else {
gF1->SetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
}
//*-*- If case of a predefined function, then compute initial values of parameters
Int_t special = gF1->GetNumber();
if (special == 100) InitGaus();
else if (special == 200) InitExpo();
else if (special == 299+npar) InitPolynom();
//*-*- Set error criterion for chisquare
arglist[0] = 1;
gMinuit->SetFCN(GraphFitChisquare);
gMinuit->mnexcm("SET ERR",arglist,1,ierf);
//*-*- Some initialisations
if (!Foption.Verbose) {
arglist[0] = -1;
gMinuit->mnexcm("SET PRINT", arglist,1,ierf);
arglist[0] = 0;
gMinuit->mnexcm("SET NOW", arglist,0,ierf);
}
//*-*- Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = gF1->GetParameter(i);
gF1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.3*TMath::Abs(par);
if (we <= TMath::Abs(par)*1e-6) we = 1;
gMinuit->mnparm(i,gF1->GetParName(i),par,we,al,bl,ierf);
}
if(nfixed > 0)gMinuit->mnexcm("FIX",arglist,nfixed,ierf); // Otto
//*-*- Reset Print level
if (!Foption.Quiet) {
if (Foption.Verbose) { arglist[0] = 2; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
else { arglist[0] = 0; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
}
//*-*- Perform minimization
SetBit(kFitInit);
arglist[0] = 5000; //MaxIterations
arglist[1] = 1e-2; //epsilon
gMinuit->mnexcm("MIGRAD",arglist,2,ierf);
if (Foption.Errors) {
gMinuit->mnexcm("HESSE",arglist,0,ierf);
gMinuit->mnexcm("MINOS",arglist,0,ierf);
}
//*-*- Get return status
for (i=0;i<npar;i++) {
gMinuit->mnpout(i,gF1->GetParName(i), par,we,al,bl,ierf);
if (Foption.Errors) werr = we;
else {
gMinuit->mnerrs(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
gF1->SetParameter(i,par);
gF1->SetParError(i,werr);
}
gMinuit->mnstat(amin,edm,errdef,nvpar,nparx,icstat);
gF1->SetChisquare(amin);
//*-*- Print final values of parameters.
if (!Foption.Quiet) {
if (Foption.Errors) gMinuit->mnprin(4,amin);
else gMinuit->mnprin(3,amin);
}
delete [] arglist;
//*-*- Store fitted function in histogram functions list and draw
if (!Foption.Nostore) {
if (!Foption.Plus) fFunctions->Delete();
fnew1 = new TF1();
gF1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax);
if (TestBit(kCanDelete)) return;
if (gPad) gPad->Modified();
}
}
//______________________________________________________________________________
void TGraph::FitPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph fit options*-*-*-*-*-*
//*-* ==========================================
//
// See class TFitPanel for example
if (gPad) {
gROOT->SetSelectedPrimitive(gPad->GetSelected());
gROOT->SetSelectedPad(gPad->GetSelectedPad());
}
TList *lc = (TList*)gROOT->GetListOfCanvases();
if (!lc->FindObject("fitpanelgraph")) {
char cmd[] = "TFitPanelGraph *fitpanel = new TFitPanelGraph("fitpanelgraph","Fit Panel",300,400);";
gInterpreter->ProcessLine(cmd);
return;
}
char cmdupd[] = "fitpanelgraph->SetDefaults(); fitpanelgraph->Show();";
gInterpreter->ProcessLine(cmdupd);
}
//______________________________________________________________________________
Float_t TGraph::GetErrorX(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
Float_t TGraph::GetErrorY(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
TH1F *TGraph::GetHistogram()
{
// Returns a pointer to the histogram used to draw the axis
// Takes into account the two following cases.
// 1- option 'A' was specified in TGraph::Draw. Return fHistogram
// 2- user had called TPad::DrawFrame. return pointer to hframe histogram
if (fHistogram) return fHistogram;
if (!gPad) return 0;
gPad->Modified();
gPad->Update();
if (fHistogram) return fHistogram;
TH1F *h1 = (TH1F*)gPad->GetPrimitive("hframe");
return h1;
}
//______________________________________________________________________________
void TGraph::GetPoint(Int_t i, Float_t &x, Float_t &y)
{
//*-*-*-*-*-*-*-*-*-*-*Get x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0 || i >= fNpoints) return;
if (!fX || !fY) return;
x = fX[i];
y = fY[i];
}
//______________________________________________________________________________
TAxis *TGraph::GetXaxis()
{
// Get x axis of the graph.
if (fHistogram) return fHistogram->GetXaxis();
return 0;
}
//______________________________________________________________________________
TAxis *TGraph::GetYaxis()
{
// Get y axis of the graph.
if (fHistogram) return fHistogram->GetYaxis();
return 0;
}
//______________________________________________________________________________
void GraphFitChisquare(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag)
{
//*-*-*-*-*-*Minimization function for Graphs using a Chisquare method*-*-*-*-*
//*-* =========================================================
Double_t cu,eu,fu,fsum;
Double_t dersum[25], grad[25];
static Double_t eysum[50];
Double_t x[1];
Float_t errormax;
Int_t bin, k, npfits, nparts, part;
TGraph *gr = (TGraph*)gMinuit->GetObjectFit();
Int_t n = gr->GetN();
Float_t *gx = gr->GetX();
Float_t *gy = gr->GetY();
npar = gF1->GetNpar();
Float_t cumin = gy[0];
Float_t cumax = gy[0];
if (flag == 2) for (k=0;k<npar;k++) dersum[k] = gin[k] = 0;
nparts = n/3;
if (nparts == 0) nparts = 1;
if (nparts > 40) nparts = 40;
Float_t fxmin = gF1->GetXmin();
Float_t fxmax = gF1->GetXmax();
Float_t dfx = (fxmax - fxmin)/nparts;
if (gr->TestBit(kFitInit)) {
for (part=0;part<nparts;part++) { eysum[part] = 0;}
}
gF1->InitArgs(x,u);
npfits = 0;
f = 0;
for (bin=0;bin<n;bin++) {
x[0] = gx[bin];
if (Foption.Range) {
if (x[0] < fxmin) continue;
if (x[0] > fxmax) continue;
}
cu = gy[bin];
fu = gF1->EvalPar(x,u);
eu = gr->GetErrorY(bin);
if (Foption.W1) eu = 1;
if (eu < 0) {
part = Int_t((x[0] - fxmin)/dfx);
if (part < 0) part = 0;
if (part >= nparts) part = nparts-1;
if (gr->TestBit(kFitInit)) {
eysum[part] += (cu-fu)*(cu-fu);
if (cu < cumin) cumin = cu;
if (cu > cumax) cumax = cu;
} else {
eu = eysum[part];
}
}
if (flag == 2) {
for (k=0;k<npar;k++) dersum[k] += 1; //should be the derivative
}
npfits++;
if (flag == 2) {
for (k=0;k<npar;k++) grad[k] += dersum[k]*(fu-cu)/eu; dersum[k] = 0;
}
if (eu) fsum = (cu-fu)/eu;
else fsum = cu-fu;
f += fsum*fsum;
}
// make a better error estimate to be used in the next iterations
if (gr->TestBit(kFitInit)) {
gr->ResetBit(kFitInit);
errormax = 0.2*(cumax-cumin);
for (part=0;part<nparts;part++) {
eysum[part] = TMath::Sqrt(eysum[part]);
if (eysum[part] > errormax) eysum[part] = errormax;
if (errormax < 0.2) eysum[part] = 1;
}
}
gF1->SetNumberFitPoints(npfits);
}
//______________________________________________________________________________
void TGraph::InitGaus()
{
//*-*-*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
//*-* ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
static Double_t sqrtpi = 2.506628;
//*-*- Compute mean value and RMS of the graph in the given range
allcha = sumx = sumx2 = 0;
for (bin=0;bin<fNpoints;bin++) {
x = fX[bin];
val = fY[bin];
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
Float_t binwidx = TMath::Abs((fX[fNpoints-1] - fX[0])/fNpoints);
if (rms == 0) rms = 1;
gF1->SetParameter(0,binwidx*allcha/(sqrtpi*rms));
gF1->SetParameter(1,mean);
gF1->SetParameter(2,rms);
}
//______________________________________________________________________________
void TGraph::InitExpo()
{
//*-*-*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
//*-* =======================================================
Double_t constant, slope;
Int_t ifail;
Int_t nchanx = xlast - xfirst + 1;
LeastSquareLinearFit(-nchanx, constant, slope, ifail);
gF1->SetParameter(0,constant);
gF1->SetParameter(1,slope);
}
//______________________________________________________________________________
void TGraph::InitPolynom()
{
//*-*-*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
//*-* ===================================================
Double_t fitpar[25];
Int_t nchanx = xlast - xfirst + 1;
Int_t npar = gF1->GetNpar();
LeastSquareFit( nchanx, npar, fitpar);
for (Int_t i=0;i<npar;i++) gF1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void TGraph::LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
//*-*-*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
//*-* =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
//
static Double_t zero = 0.;
static Double_t one = 1.;
static Int_t idim = 20;
static Double_t b[400] /* was [20][20] */;
static Int_t i, k, l, ifail;
static Double_t power;
static Double_t da[20], xk, yk;
if (m <= 2) {
LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Float_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
for (k = 0; k < fNpoints; ++k) {
xk = fX[k];
yk = fY[k];
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
if (ifail < 0) {
a[0] = fY[0];
for (i=1; i<m; ++i) a[i] = 0;
return;
}
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void TGraph::LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
//*-*-*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
//*-* =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
static Double_t xbar, ybar, x2bar;
static Int_t i, n;
static Double_t xybar;
static Float_t fn, xk, yk;
static Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
for (i = 0; i < fNpoints; ++i) {
xk = fX[i];
yk = fY[i];
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Float_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void TGraph::Paint(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ===========================================
if (strstr(option,"H") || strstr(option,"h")) {
PaintGrapHist(fNpoints, fX, fY, option);
} else {
PaintGraph(fNpoints, fX, fY, option);
}
TObject *f;
if (fFunctions) {
TIter next(fFunctions);
while ((f = (TObject*) next())) {
if (f->IsA() == TF1::Class()) f->Paint("lsame");
else f->Paint();
}
}
}
//______________________________________________________________________________
void TGraph::PaintGraph(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Control function to draw a graph*-*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or X(2) : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or Y(2) : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='F' : A fill area is drawn ('CF' draw a smooth fill area)
//
// chopt='A' : Axis are drawn around the graph
//
// chopt='C' : A smooth Curve is drawn
//
// chopt='*' : A Star is plotted at each point
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart is drawn at each point
//
// chopt='1' : ylow=rwymin
//
//
Int_t OptionLine , OptionAxis , OptionCurve,OptionStar ,OptionMark;
Int_t OptionBar , OptionR , OptionOne;
Int_t OptionFill , OptionZ ,OptionCurveFill;
Int_t i, npt, nloop;
Int_t drawtype;
Float_t xlow, xhigh, ylow, yhigh;
Float_t barxmin, barxmax, barymin, barymax;
Float_t uxmin, uxmax;
Float_t x1, xn, y1, yn;
Float_t dbar, bdelta;
//*-* ______________________________________
if (npoints <= 0) {
Error("PaintGraph", "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("R")) OptionR = 1; else OptionR = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
OptionZ = 0;
//*-* If no "drawing" option is selected and if chopt<>' '
//*-* nothing is done.
if (OptionLine+OptionFill+OptionCurve+OptionStar+OptionMark+OptionBar == 0) {
if (strlen(chopt) == 0) OptionLine=1;
else return;
}
if (OptionStar) SetMarkerStyle(3);
OptionCurveFill = 0;
if (OptionCurve && OptionFill) {
OptionCurveFill = 1;
OptionFill = 0;
}
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- Draw the Axis with a fixed number of division: 510
Float_t rwxmin,rwxmax, rwymin, rwymax, maximum, minimum;
if (OptionAxis) {
rwxmin = rwxmax = x[0];
rwymin = rwymax = y[0];
for (i=1;i<npoints;i++) {
if (x[i] < rwxmin) rwxmin = x[i];
if (x[i] > rwxmax) rwxmax = x[i];
if (y[i] < rwymin) rwymin = y[i];
if (y[i] > rwymax) rwymax = y[i];
}
ComputeRange(rwxmin, rwymin, rwxmax, rwymax); //this is redefined in TGraphErrors
if (rwxmin == rwxmax) rwxmax += 1.;
if (rwymin == rwymax) rwymax += 1.;
Float_t dx = 0.1*(rwxmax-rwxmin);
Float_t dy = 0.1*(rwymax-rwymin);
uxmin = rwxmin - dx;
uxmax = rwxmax + dx;
minimum = rwymin - dy;
maximum = rwymax + dy;
if (fMinimum != -1111) rwymin = minimum = fMinimum;
if (fMaximum != -1111) rwymax = maximum = fMaximum;
if (uxmin < 0 && rwxmin >= 0) {
if (gPad->GetLogx()) uxmin = 0.9*rwxmin;
else uxmin = 0;
}
if (uxmax > 0 && rwxmax <= 0) {
if (gPad->GetLogx()) uxmax = 1.1*rwxmax;
else uxmax = 0;
}
if (minimum < 0 && rwymin >= 0) {
if(gPad->GetLogy()) minimum = 0.9*rwymin;
else minimum = 0;
}
if (maximum > 0 && rwymax <= 0) {
if(gPad->GetLogy()) maximum = 1.1*rwymax;
else maximum = 0;
}
if (minimum <= 0 && gPad->GetLogy()) minimum = 0.001*maximum;
if (uxmin <= 0 && gPad->GetLogx()) {
if (uxmax > 1000) uxmin = 1;
else uxmin = 0.001*uxmax;
}
rwxmin = uxmin;
rwxmax = uxmax;
rwymin = minimum;
rwymax = maximum;
if (fHistogram) {
fHistogram->SetMinimum(rwymin);
fHistogram->SetMaximum(rwymax);
fHistogram->GetXaxis()->SetLimits(rwxmin,rwxmax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
}
//*-*- Create a temporary histogram and fill each channel with the function value
if (!fHistogram) {
fHistogram = new TH1F((char*)GetName(),(char*)GetTitle(),40,rwxmin,rwxmax);
if (!fHistogram) return;
fHistogram->SetMinimum(rwymin);
fHistogram->SetBit(kNoStats);
fHistogram->SetMaximum(rwymax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
fHistogram->SetDirectory(0);
}
fHistogram->Paint();
}
TF1 *fit = 0;
if (fFunctions) fit = (TF1*)fFunctions->First();
if (fit) {
if (fHistogram) {
fHistogram->PaintStat(0,fit);
} else {
TH1F *hfit = new TH1F("___0","",2,0,1);
hfit->PaintStat(0,fit);
delete hfit;
}
}
rwxmin = gPad->GetUxmin();
rwxmax = gPad->GetUxmax();
rwymin = gPad->GetUymin();
rwymax = gPad->GetUymax();
uxmin = gPad->PadtoX(rwxmin);
uxmax = gPad->PadtoX(rwxmax);
if (fHistogram) {
maximum = fHistogram->GetMaximum();
minimum = fHistogram->GetMinimum();
} else {
maximum = gPad->PadtoY(rwymax);
minimum = gPad->PadtoY(rwymin);
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Draw the graph with a polyline or a fill area
if (OptionLine || OptionFill) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
nloop = npoints;
if (OptionFill && (xn != x1 || yn != y1)) nloop++;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == nloop) {
ComputeLogs(npt, OptionZ);
Int_t bord = gStyle->GetDrawBorder();
if (OptionR) {
if (OptionFill) {
gPad->PaintFillArea(npt,yworkl,xworkl);
if (bord) gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else {
if (OptionFill) {
gPad->PaintFillArea(npt,xworkl,yworkl);
if (bord) gPad->PaintPolyLine(npt,xworkl,yworkl);
}
else gPad->PaintPolyLine(npt,xworkl,yworkl);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
}
}
//*-*- Draw the graph with a smooth Curve. Smoothing via Smooth
if (OptionCurve) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
drawtype = 1;
nloop = npoints;
if (OptionCurveFill) {
drawtype += 1000;
if (xn != x1 || yn != y1) nloop++;
}
if (!OptionR) {
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (yworkl[npt-1] < rwymin || yworkl[npt-1] > rwymax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=0;i<nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype += 10;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (xworkl[npt-1] < rwxmin || xworkl[npt-1] > rwxmax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=1;i<=nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the graph with a '*' on every points
if (OptionStar) {
SetMarkerStyle(3);
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph with the current polymarker on
//*-*- every points
if (OptionMark) {
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph as a bar chart
if (OptionBar) {
if (!OptionR) {
barxmin = x[0];
barxmax = x[0];
for (i=1;i<npoints;i++) {
if (x[i] < barxmin) barxmin = x[i];
if (x[i] > barxmax) barxmax = x[i];
}
bdelta = (barxmax-barxmin)/float(npoints);
}
else {
barymin = y[0];
barymax = y[0];
for (i=1;i<npoints;i++) {
if (y[i] < barymin) barymin = y[i];
if (y[i] > barymax) barymax = y[i];
}
bdelta = (barymax-barymin)/float(npoints);
}
dbar = 0.5*bdelta*gStyle->GetBarWidth();
if (!OptionR) {
for (i=1;i<=npoints;i++) {
xlow = x[i-1] - dbar;
xhigh = x[i-1] + dbar;
yhigh = y[i-1];
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
if (yworkl[0] < gPad->GetUymin()) yworkl[0] = gPad->GetUymin();
if (yworkl[1] < gPad->GetUymin()) continue;
if (yworkl[1] > gPad->GetUymax()) yworkl[0] = gPad->GetUymax();
if (yworkl[0] > gPad->GetUymax()) continue;
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
else {
for (i=1;i<=npoints;i++) {
xhigh = x[i-1];
ylow = y[i-1] - dbar;
yhigh = y[i-1] + dbar;
xlow = TMath::Max((Float_t)0, gPad->GetUxmin());
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::PaintGrapHist(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*Control function to draw a graphistogram*-*-*-*-*-*-*-*-*-*
//*-* ========================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or x[1] : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or y[1] : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='R' : Graph is drawn horizontaly, parallel to X axis.
// (default is vertically, parallel to Y axis)
// If option R is selected the user must give:
// 2 values for Y (y[0]=YMIN and y[1]=YMAX)
// N values for X, one for each channel.
// Otherwise the user must give:
// N values for Y, one for each channel.
// 2 values for X (x[0]=XMIN and x[1]=XMAX)
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='H' : An Histogram with equidistant bins is drawn
// as a polyline.
//
// chopt='F' : An histogram with equidistant bins is drawn
// as a fill area. Contour is not drawn unless
// chopt='H' is also selected..
//
// chopt='N' : Non equidistant bins (default is equidistant)
// If N is the number of channels array X and Y
// must be dimensionned as follow:
// If option R is not selected (default) then
// the user must give:
// (N+1) values for X (limits of channels).
// N values for Y, one for each channel.
// Otherwise the user must give:
// (N+1) values for Y (limits of channels).
// N values for X, one for each channel.
//
// chopt='F1': Idem as 'F' except that fill area is no more
// reparted arround axis X=0 or Y=0 .
//
// chopt='C' : A smooth Curve is drawn.
//
// chopt='*' : A Star is plotted at the center of each bin.
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart with equidistant bins is drawn as fill
// areas (Contours are drawn).
//
//
static const char *where = "PaintGraphHist";
const Int_t NPMXFA= 99;
Int_t OptionLine , OptionAxis , OptionCurve, OptionStar , OptionMark;
Int_t OptionBar , OptionRot , OptionOne;
Int_t OptionFill , OptionZ;
Int_t OptionHist , OptionBins , OptionMarker;
Int_t i, j, npt;
Int_t drawtype, drawborder, drawbordersav;
Float_t xlow, xhigh, ylow, yhigh;
Float_t wmin, wmax;
Float_t dbar, offset, wminstep;
Float_t delta = 0;
Float_t ylast = 0;
Float_t xi, xi1, xj, xj1, yi1, yi, yj, yj1, xwmin, ywmin;
Int_t first, last, nbins;
Int_t fillarea;
static char choptaxis[10] = " ";
//*-* ______________________________________
if (npoints <= 0) {
Error(where, "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("H")) OptionHist = 1; else OptionHist = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("R")) OptionRot = 1; else OptionRot = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("N")) OptionBins = 1; else OptionBins = 0;
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- If necessary the adresses of the vectors are saved in
//*-*- a link area.
OptionZ = 1;
if (OptionStar) SetMarkerStyle(3);
first = 1;
last = npoints;
nbins = last - first + 1;
//*-*- Draw the Axis with a fixed number of division: 510
Float_t baroffset = gStyle->GetBarOffset();
Float_t barwidth = gStyle->GetBarWidth();
Float_t rwxmin = gPad->GetUxmin();
Float_t rwxmax = gPad->GetUxmax();
Float_t rwymin = gPad->GetUymin();
Float_t rwymax = gPad->GetUymax();
Float_t uxmin = gPad->PadtoX(rwxmin);
Float_t uxmax = gPad->PadtoX(rwxmax);
Float_t rounding = (uxmax-uxmin)*1.e-5;
drawborder = gStyle->GetDrawBorder();
if (OptionAxis) {
Int_t nx1, nx2, ndivx, ndivy, ndiv;
choptaxis[0] = 0;
Float_t rwmin = rwxmin;
Float_t rwmax = rwxmax;
ndivx = gStyle->GetNdivisions("X");
ndivy = gStyle->GetNdivisions("Y");
if (ndivx > 1000) {
nx2 = ndivx/100;
nx1 = TMath::Max(1, ndivx%100);
ndivx = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsWNDC());
}
ndiv =TMath::Abs(ndivx);
if (ndivx < 0) strcat(choptaxis, "N");
if (gPad->GetGridx()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogx()) {
rwmin = TMath::Power(10,rwxmin);
rwmax = TMath::Power(10,rwxmax);
strcat(choptaxis, "G");
}
TGaxis *axis = new TGaxis();
axis->SetLineColor(gStyle->GetAxisColor("X"));
axis->SetTextColor(gStyle->GetLabelColor("X"));
axis->SetTextFont(gStyle->GetLabelFont("X"));
axis->SetLabelSize(gStyle->GetLabelSize("X"));
axis->SetLabelOffset(gStyle->GetLabelOffset("X"));
axis->SetTickSize(gStyle->GetTickLength("X"));
axis->PaintAxis(rwxmin,rwymin,rwxmax,rwymin,rwmin,rwmax,ndiv,choptaxis);
choptaxis[0] = 0;
rwmin = rwymin;
rwmax = rwymax;
if (ndivy < 0) {
nx2 = ndivy/100;
nx1 = TMath::Max(1, ndivy%100);
ndivy = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsHNDC());
strcat(choptaxis, "N");
}
ndiv =TMath::Abs(ndivy);
if (gPad->GetGridy()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogy()) {
rwmin = TMath::Power(10,rwymin);
rwmax = TMath::Power(10,rwymax);
strcat(choptaxis,"G");
}
axis->SetLineColor(gStyle->GetAxisColor("Y"));
axis->SetTextColor(gStyle->GetLabelColor("Y"));
axis->SetTextFont(gStyle->GetLabelFont("Y"));
axis->SetLabelSize(gStyle->GetLabelSize("Y"));
axis->SetLabelOffset(gStyle->GetLabelOffset("Y"));
axis->SetTickSize(gStyle->GetTickLength("Y"));
axis->PaintAxis(rwxmin,rwymin,rwxmin,rwymax,rwmin,rwmax,ndiv,choptaxis);
delete axis;
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Min-Max scope
if (!OptionRot) {wmin = x[0]; wmax = x[1];}
else {wmin = y[0]; wmax = y[1];}
if (!OptionBins) delta = (wmax - wmin)/ float(nbins);
//*-*- Draw the histogram with a fill area
if (OptionFill && !OptionCurve) {
fillarea = kTRUE;
if (!OptionRot) {
xwork[0] = wmin;
if (!OptionOne) ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
else ywork[0] = gPad->GetUymin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((j-first+1)*delta);
}
else {
xj1 = x[j]; xj = x[j-1];
if (xj1 < xj) {
if (j != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j];
}
ywork[npt-1] = y[j-1];
ywork[npt] = y[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (j == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
xwork[0] = xwork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++) {
}
else {
ywork[0] = wmin;
if (!OptionOne) xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
else xwork[0] = gPad->GetUxmin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((j-first+1)*delta);
}
else {
yj1 = y[j]; yj = y[j-1];
if (yj1 < yj) {
if (j != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[j-1]; ywork[npt] = y[j];
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (j == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
ywork[0] = ywork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++)
}
}
//*-*- Draw a standard Histogram (default)
if ((OptionHist) || strlen(chopt) == 0) {
if (!OptionRot) {
xwork[0] = wmin;
// ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
ywork[0] = gPad->GetUymin();
ywmin = ywork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((i-first+1)*delta);
}
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i];
}
ywork[npt-1] = y[i-1];
ywork[npt] = y[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (i == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
else {
ywork[0] = wmin;
xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
xwmin = xwork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((i-first+1)*delta);
}
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1]; ywork[npt] = y[i];
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (i == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
}
//*-*- Draw the histogram with a smooth Curve. The computing
//*-*- of the smoothing is done by the routine IGRAP1
if (OptionCurve) {
if (!OptionFill) drawtype = 1;
else {
if (!OptionOne) drawtype = 2;
else drawtype = 3;
}
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
ComputeLogs(npt, OptionZ);
if ((yworkl[npt] < rwymin) || (yworkl[npt] > rwymax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype = drawtype+10;
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
ComputeLogs(npt, OptionZ);
if ((xworkl[npt] < uxmin) || (xworkl[npt] > uxmax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the histogram with a simple line
OptionMarker = 0;
if ((OptionStar) || (OptionMark))OptionMarker=1;
if ((OptionMarker) || (OptionLine)) {
wminstep = wmin + 0.5*delta;
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wminstep + (i-first)*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
if ((ywork[npt-1] < rwymin) || (ywork[npt-1] > rwymax)) {
if ((ywork[npt-1] < rwymin)) ywork[npt-1] = rwymin;
if ((ywork[npt-1] > rwymax)) ywork[npt-1] = rwymax;
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
else {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wminstep+(i-first)*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
if ((xwork[npt-1] < uxmin) || (xwork[npt-1] > uxmax)) {
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine != 0 && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
}
//*-*- Draw the histogram as a bar chart
if (OptionBar) {
if (!OptionBins) { offset = delta*baroffset; dbar = delta*barwidth; }
else {
if (!OptionRot) {
offset = (x[1]-x[0])*baroffset;
dbar = (x[1]-x[0])*barwidth;
} else {
offset = (y[1]-y[0])*baroffset;
dbar = (y[1]-y[0])*barwidth;
}
}
drawbordersav = drawborder;
gStyle->SetDrawBorder(1);
if (!OptionRot) {
xlow = wmin+offset;
xhigh = wmin+offset+dbar;
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
for (i=first; i<=last;i++) {
yhigh = y[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
if (!OptionBins) {
xlow = xlow+delta;
xhigh = xhigh+delta;
}
else {
if (i < last) {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
Error(where, "X must be in increasing order");
return;
}
offset = (x[i+1]-x[i])*baroffset;
dbar = (x[i+1]-x[i])*barwidth;
xlow = x[i] + offset;
xhigh = x[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
else {
ylow = wmin + offset;
yhigh = wmin + offset + dbar;
if (!OptionOne) xlow = TMath::Max((Float_t)0,gPad->GetUxmin());
else xlow = gPad->GetUxmin();
for (i=first; i<=last;i++) {
xhigh = x[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
gPad->PaintBox(xlow,ylow,xhigh,yhigh);
if (!OptionBins) {
ylow = ylow + delta;
yhigh = yhigh + delta;
}
else {
if (i < last) {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
Error(where, "Y must be in increasing order");
return;
}
offset = (y[i+1]-y[i])*baroffset;
dbar = (y[i+1]-y[i])*barwidth;
ylow = y[i] + offset;
yhigh = y[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
gStyle->SetDrawBorder(drawbordersav);
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::ComputeLogs(Int_t npoints, Int_t opt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Convert WC from Log scales*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==========================
//
// Take the LOG10 of xwork and ywork according to the value of Options
// and put it in xworkl and yworkl.
//
// npoints : Number of points in xwork and in ywork.
//
for (Int_t i=0;i<npoints;i++) {
xworkl[i] = xwork[i];
yworkl[i] = ywork[i];
if (gPad->GetLogx()) {
if (xworkl[i] > 0) xworkl[i] = TMath::Log10(xworkl[i]);
else xworkl[i] = gPad->GetX1();
}
if (!opt && gPad->GetLogy()) {
if (yworkl[i] > 0) yworkl[i] = TMath::Log10(yworkl[i]);
else yworkl[i] = gPad->GetY1();
}
// if (yworkl[i] > gPad->GetUymax()) yworkl[i] = gPad->GetUymax();
}
}
//______________________________________________________________________________
void TGraph::Print(Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Print graph values*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==================
for (Int_t i=0;i<fNpoints;i++) {
printf("x[%d]=%g, y[%d]=%gn",i,fX[i],i,fY[i]);
}
}
//______________________________________________________________________________
void TGraph::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
char quote = '"';
out<<" "<<endl;
if (gROOT->ClassSaved(TGraph::Class())) {
out<<" ";
} else {
out<<" TGraph *";
}
out<<"graph = new TGraph("<<fNpoints<<");"<<endl;
out<<" graph->SetName("<<quote<<GetName()<<quote<<");"<<endl;
out<<" graph->SetTitle("<<quote<<GetTitle()<<quote<<");"<<endl;
SaveFillAttributes(out,"graph",0,1001);
SaveLineAttributes(out,"graph",1,1,1);
SaveMarkerAttributes(out,"graph",1,1,1);
for (Int_t i=0;i<fNpoints;i++) {
out<<" graph->SetPoint("<<i<<","<<fX[i]<<","<<fY[i]<<");"<<endl;
}
out<<" graph->Draw("
<<quote<<option<<quote<<");"<<endl;
}
//______________________________________________________________________________
void TGraph::SetMaximum(Float_t maximum)
{
fMaximum = maximum;
if (fHistogram) fHistogram->SetMaximum(maximum);
}
//______________________________________________________________________________
void TGraph::SetMinimum(Float_t minimum)
{
fMinimum = minimum;
if (fHistogram) fHistogram->SetMinimum(minimum);
}
//______________________________________________________________________________
void TGraph::SetPoint(Int_t i, Float_t x, Float_t y)
{
//*-*-*-*-*-*-*-*-*-*-*Set x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0) return;
if (i >= fNpoints) {
// re-allocate the object
Float_t *savex = new Float_t[i+1];
Float_t *savey = new Float_t[i+1];
if (fNpoints > 0) {
memcpy(savex,fX,fNpoints*sizeof(Float_t));
memcpy(savey,fY,fNpoints*sizeof(Float_t));
}
if (fX) delete [] fX;
if (fY) delete [] fY;
fX = savex;
fY = savey;
fNpoints = i+1;
}
fX[i] = x;
fY[i] = y;
}
//______________________________________________________________________________
void TGraph::Smooth(Int_t npoints, Float_t *x, Float_t *y, Int_t drawtype)
{
//*-*-*-*-*-*-*-*-*-*-*-*Smooth a curve given by N points*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
// Underlaying routine for Draw based on the CERN GD3 routine TVIPTE
//
// Author - Marlow etc. Modified by - P. Ward Date - 3.10.1973
//
// This routine draws a smooth tangentially continuous curve through
// the sequence of data points P(I) I=1,N where P(I)=(X(I),Y(I))
// the curve is approximated by a polygonal arc of short vectors .
// the data points can represent open curves, P(1) != P(N) or closed
// curves P(2) == P(N) . If a tangential discontinuity at P(I) is
// required , then set P(I)=P(I+1) . loops are also allowed .
//
// Reference Marlow and Powell,Harwell report No.R.7092.1972
// MCCONALOGUE,Computer Journal VOL.13,NO4,NOV1970PP392 6
//
// _Input parameters:
//
// npoints : Number of data points.
// x : Abscissa
// y : Ordinate
//
//
// delta is the accuracy required in constructing the curve.
// if it is zero then the routine calculates a value other-
// wise it uses this value. (default is 0.0)
//
//
Int_t i, k, kp, km, NpointsMax, banksize, n2, npt;
Int_t maxiterations, finished;
Int_t jtype, ktype, closed;
Float_t sxmin, sxmax, symin, symax;
Float_t delta;
Float_t xorg, yorg;
Float_t ratio_signs, xratio, yratio;
Int_t flgic, flgis;
Int_t iw, loptx;
Float_t P1, P2, P3, P4, P5, P6;
Float_t W1, W2, W3;
Float_t A, B, C, R, S, T, Z;
Float_t CO, SO, CT, ST, CTU, STU, XNT;
Float_t DX1, DY1, DX2, DY2, DK1, DK2;
Float_t XO, YO, DX, DY, XT, YT;
Float_t XA, XB, YA, YB;
Float_t U1, U2, U3, TJ;
Float_t CC, ERR;
Float_t SB, STH;
Float_t wsign, tsquare, tcube;
C = T = CO = SO = CT = ST = CTU = STU = DX1 = DY1 = DX2 = DY2 = 0;
XT = YT = XA = XB = YA = YB = U1 = U2 = U3 = TJ = SB = 0;
//*-* ______________________________________
NpointsMax = npoints*10;
n2 = NpointsMax-2;
banksize = n2;
Float_t *qlx = new Float_t[NpointsMax];
Float_t *qly = new Float_t[NpointsMax];
if (!qlx || !qly) {
Error("Smooth", "not enough space in memory");
return;
}
//*-*- Decode the type of curve according to
//*-*- chopt of IGHIST.
//*-*- ('S', 'SA', 'SA1' ,'XS', 'XSA', or 'XSA1')
if (drawtype >= 1000) drawtype -= 1000;
loptx = kFALSE;
jtype = drawtype-10;
if (jtype > 0) { ktype = jtype; loptx = kTRUE; }
else ktype = drawtype;
Float_t ruxmin = gPad->GetUxmin();
Float_t ruymin = gPad->GetUymin();
if (ktype == 3) {
xorg = ruxmin;
yorg = ruymin;
} else {
xorg = TMath::Max((Float_t)0,ruxmin);
yorg = TMath::Max((Float_t)0,ruymin);
}
maxiterations = 20;
delta = 0.00055;
//*-*- Scale data to the range 0-ratio_signs in X, 0-1 in Y
//*-*- where ratio_signs is the ratio between the number of changes
//*-*- of sign in Y divided by the number of changes of sign in X
sxmin = x[0];
sxmax = x[0];
symin = y[0];
symax = y[0];
Float_t six = 1;
Float_t siy = 1;
for (i=1;i<npoints;i++) {
if (i > 1) {
if ((x[i]-x[i-1])*(x[i-1]-x[i-2]) < 0) six++;
if ((y[i]-y[i-1])*(y[i-1]-y[i-2]) < 0) siy++;
}
if (x[i] < sxmin) sxmin = x[i];
if (x[i] > sxmax) sxmax = x[i];
if (y[i] < symin) symin = y[i];
if (y[i] > symax) symax = y[i];
}
closed = 0;
Float_t dx1n = TMath::Abs(x[npoints-1]-x[0]);
Float_t dy1n = TMath::Abs(y[npoints-1]-y[0]);
if (dx1n < 0.01*(sxmax-sxmin) && dy1n < 0.01*(symax-symin)) closed = 1;
if (sxmin == sxmax) xratio = 1;
else {
if (six > 1) ratio_signs = siy/six;
else ratio_signs = 20;
xratio = ratio_signs/(sxmax-sxmin);
}
if (symin == symax) yratio = 1;
else yratio = 1/(symax-symin);
qlx[0] = x[0];
qly[0] = y[0];
for (i=0;i<npoints;i++) {
x[i] = (x[i]-sxmin)*xratio;
y[i] = (y[i]-symin)*yratio;
}
//*-*- finished is minus one if we must draw a straight line from P(k-1)
//*-*- to P(k). finished is one if the last call to IPL has < N2
//*-*- points. finished is zero otherwise. npt counts the X and Y
//*-*- coordinates in work . When npt=N2 a call to IPL is made.
finished = 0;
npt = 1;
k = 1;
//*-*- Convert coordinates back to original system
//*-*- Separate the set of data points into arcs P(k-1),P(k).
//*-*- Calculate the direction cosines. first consider whether
//*-*- there is a continuous tangent at the endpoints.
if (!closed) {
if (x[0] != x[npoints-1] || y[0] != y[npoints-1]) goto L40;
if (x[npoints-2] == x[npoints-1] && y[npoints-2] == y[npoints-1]) goto L40;
if (x[0] == x[1] && y[0] == y[1]) goto L40;
}
flgic = kFALSE;
flgis = kTRUE;
//*-*- flgic is true if the curve is open and false if it is closed.
//*-*- flgis is true in the main loop, but is false if there is
//*-*- a deviation from the main loop.
km = npoints - 1;
//*-*- Calculate direction cosines at P(1) using P(N-1),P(1),P(2).
goto L100;
L40:
flgic = kTRUE;
flgis = kFALSE;
//*-*- Skip excessive consecutive equal points.
L50:
if (k >= npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
k++;
if (x[k-1] == x[k-2] && y[k-1] == y[k-2]) goto L50;
L60:
km = k-1;
if (k > npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
if (k < npoints) goto L90;
if (!flgic) { kp = 2; goto L130;}
L80:
if (flgis) goto L150;
//*-*- Draw a straight line from P(k-1) to P(k).
finished = -1;
goto L170;
//*-*- Test whether P(k) is a cusp.
L90:
if (x[k-1] == x[k] && y[k-1] == y[k]) goto L80;
L100:
kp = k+1;
goto L130;
//*-*- Branch if the next section of the curve begins at a cusp.
L110:
if (!flgis) goto L50;
//*-*- Carry forward the direction cosines from the previous arc.
L120:
CO = CT;
SO = ST;
k++;
goto L60;
//*-*- Calculate the direction cosines at P(k). If k=1 then
//*-*- N-1 is used for k-1. If k=N then 2 is used for k+1.
//*-*- direction cosines at P(k) obtained from P(k-1),P(k),P(k+1).
L130:
DX1 = x[k-1] - x[km-1];
DY1 = y[k-1] - y[km-1];
DK1 = DX1*DX1 + DY1*DY1;
DX2 = x[kp-1] - x[k-1];
DY2 = y[kp-1] - y[k-1];
DK2 = DX2*DX2 + DY2*DY2;
CTU = DX1*DK2 + DX2*DK1;
STU = DY1*DK2 + DY2*DK1;
XNT = CTU*CTU + STU*STU;
//*-*- If both ctu and stu are zero,then default.This can
//*-*- occur when P(k)=P(k+1). I.E. A loop.
if (XNT < 1.E-25) {
CTU = DY1;
STU =-DX1;
XNT = DK1;
}
//*-*- Normalise direction cosines.
CT = CTU/TMath::Sqrt(XNT);
ST = STU/TMath::Sqrt(XNT);
if (flgis) goto L160;
//*-*- Direction cosines at P(k-1) obtained from P(k-1),P(k),P(k+1).
W3 = 2*(DX1*DY2-DX2*DY1);
CO = CTU+W3*DY1;
SO = STU-W3*DX1;
XNT = 1/TMath::Sqrt(CO*CO+SO*SO);
CO = CO*XNT;
SO = SO*XNT;
flgis = kTRUE;
goto L170;
//*-*- Direction cosines at P(k) obtained from P(k-2),P(k-1),P(k).
L150:
W3 = 2*(DX1*DY2-DX2*DY1);
CT = CTU-W3*DY2;
ST = STU+W3*DX2;
XNT = 1/TMath::Sqrt(CT*CT+ST*ST);
CT = CT*XNT;
ST = ST*XNT;
flgis = kFALSE;
goto L170;
L160:
if (k <= 1) goto L120;
//*-*- For the arc between P(k-1) and P(k) with direction cosines CO,
//*-*- SO and CT,ST respectively, calculate the coefficients of the
//*-*- parametric cubic represented by X(T) and Y(T) where
//*-*- X(T)=XA*T**3 + XB*T**2 + CO*T + XO
//*-*- Y(T)=YA*T**3 + YB*T**2 + SO*T + YO
L170:
XO = x[k-2];
YO = y[k-2];
DX = x[k-1] - XO;
DY = y[k-1] - YO;
//*-*- Initialise the values of X(TI),Y(TI) in XT and YT respectively.
XT = XO;
YT = YO;
if (finished < 0) { //*-*- Draw a straight line between (XO,YO) and (XT,YT)
XT += DX;
YT += DY;
goto L300;
}
C = DX*DX+DY*DY;
A = CO+CT;
B = SO+ST;
R = DX*A+DY*B;
T = C*6/(TMath::Sqrt(R*R+2*(7-CO*CT-SO*ST)*C)+R);
tsquare = T*T;
tcube = T*tsquare;
XA = (A*T-2*DX)/tcube;
XB = (3*DX-(CO+A)*T)/tsquare;
YA = (B*T-2*DY)/tcube;
YB = (3*DY-(SO+B)*T)/tsquare;
//*-*- If the curve is close to a straight line then use a straight
//*-*- line between (XO,YO) and (XT,YT).
if (.75*TMath::Max(TMath::Abs(DX*SO-DY*CO),TMath::Abs(DX*ST-DY*CT)) <= delta) {
finished = -1;
XT += DX;
YT += DY;
goto L300;
}
//*-*- Calculate a set of values 0 == T(0).LTCT(1) < ... < T(M)=TC
//*-*- such that polygonal arc joining X(T(J)),Y(T(J)) (J=0,1,..M)
//*-*- is within the required accuracy of the curve
TJ = 0;
U1 = YA*XB-YB*XA;
U2 = YB*CO-XB*SO;
U3 = SO*XA-YA*CO;
//*-*- Given T(J), calculate T(J+1). The values of X(T(J)),
//*-*- Y(T(J)) T(J) are contained in XT,YT and TJ respectively.
L180:
S = T - TJ;
iw = -2;
//*-*- Define iw here later.
P1 = (2*U1)*TJ-U3;
P2 = (U1*TJ-U3)*3*TJ+U2;
P3 = 3*TJ*YA+YB;
P4 = (P3+YB)*TJ+SO;
P5 = 3*TJ*XA+XB;
P6 = (P5+XB)*TJ+CO;
//*-*- Test D(TJ,THETA). A is set to (Y(TJ+S)-Y(TJ))/S.B is
//*-*- set to (X(TJ+S)-X(TJ))/S.
CC = 0.8209285;
ERR = 0.1209835;
L190:
iw -= 2;
L200:
A = (S*YA+P3)*S+P4;
B = (S*XA+P5)*S+P6;
//*-*- Set Z to PSI(D/delta)-CC.
W1 = -S*(S*U1+P1);
W2 = S*S*U1-P2;
W3 = 1.5*W1+W2;
//*-*- Set the estimate of (THETA-TJ)/S.Then set the numerator
//*-*- of the expression (EQUATION 4.4)/S. Then set the square
//*-*- of D(TJ,TJ+S)/delta. Then replace Z by PSI(D/delta)-CC.
if (W3 > 0) wsign = TMath::Abs(W1);
else wsign = -TMath::Abs(W1);
STH = 0.5+wsign/(3.4*TMath::Abs(W1)+5.2*TMath::Abs(W3));
Z = S*STH*(S-S*STH)*(W1*STH+W1+W2);
Z = Z*Z/((A*A+B*B)*(delta*delta));
Z = (Z+2.642937)*Z/((.3715652*Z+3.063444)*Z+.2441889)-CC;
//*-*- Branch if Z has been calculated
if (iw > 0) goto L250;
if (Z > ERR) goto L240;
goto L220;
L210:
iw -= 2;
L220:
if (iw+2 == 0) goto L190;
if (iw+2 > 0) goto L290;
//*-*- Last part of arc.
L230:
XT = x[k-1];
YT = y[k-1];
S = 0;
goto L300;
//*-*- Z(S). find a value of S where 0 <= S <= SB such that
//*-*- TMath::Abs(Z(S)) < ERR
L240:
kp = 0;
C = Z;
SB = S;
L250:
Zero(kp,0,SB,ERR,S,Z,maxiterations);
if (kp == 2) goto L210;
if (kp > 2) {
Error("Smooth", "Attempt to plot outside plot limits");
goto L230;
}
if (iw > 0) goto L200;
//*-*- Set Z=Z(S) for S=0.
if (iw < 0) {
Z = -CC;
iw = 0;
goto L250;
}
//*-*- Set Z=Z(S) for S=SB.
Z = C;
iw = 1;
goto L250;
//*-*- Update TJ,XT and YT.
L290:
XT = XT + S*B;
YT = YT + S*A;
TJ = S + TJ;
//*-*- Convert coordinates to original system
L300:
qlx[npt] = sxmin + XT/xratio;
qly[npt] = symin + YT/yratio;
npt++;
//*-*- If a fill area must be drawn and if the banks LX and
//*-*- LY are too small they are enlarged in order to draw
//*-*- the filled area in one go.
if (npt < banksize) goto L320;
if (drawtype >= 1000 || ktype > 1) {
Int_t newsize = banksize + n2;
Float_t *qtemp = new Float_t[banksize];
for (i=0;i<banksize;i++) qtemp[i] = qlx[i];
delete [] qlx;
qlx = new Float_t[newsize];
for (i=0;i<banksize;i++) qlx[i] = qtemp[i];
for (i=0;i<banksize;i++) qtemp[i] = qly[i];
delete [] qly;
qly = new Float_t[newsize];
for (i=0;i<banksize;i++) qly[i] = qtemp[i];
delete [] qtemp;
banksize = newsize;
goto L320;
}
//*-*- Draw the graph
L310:
if (drawtype >= 1000) {
gPad->PaintFillArea(npt,qlx,qly, "B");
}
else {
if (ktype > 1) {
if (!loptx) {
qlx[npt] = qlx[npt-1];
qlx[npt+1] = qlx[0];
qly[npt] = yorg;
qly[npt+1] = yorg;
}
else {
qlx[npt] = xorg;
qlx[npt+1] = xorg;
qly[npt] = qly[npt-1];
qly[npt+1] = qly[0];
}
gPad->PaintFillArea(npt+2,qlx,qly);
}
gPad->PaintPolyLine(npt,qlx,qly);
}
npt = 1;
qlx[0] = sxmin + XT/xratio;
qly[0] = symin + YT/yratio;
L320:
if (finished > 0) goto L390;
if (finished < 0) { finished = 0; goto L110;}
if (S > 0) goto L180;
goto L110;
//*-*- Convert coordinates back to original system
L390:
for (i=0;i<npoints;i++) {
x[i] = sxmin + x[i]/xratio;
y[i] = symin + y[i]/yratio;
}
delete [] qlx;
delete [] qly;
}
//______________________________________________________________________________
void TGraph::Streamer(TBuffer &b)
{
// Stream an object of class TGraph.
if (b.IsReading()) {
b.ReadVersion(); //Version_t v = b.ReadVersion();
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNpoints;
fX = new Float_t[fNpoints];
fY = new Float_t[fNpoints];
b.ReadFastArray(fX,fNpoints);
b.ReadFastArray(fY,fNpoints);
b >> fFunctions;
b >> fHistogram;
if (fHistogram) fHistogram->SetDirectory(0);
b >> fMinimum;
b >> fMaximum;
} else {
b.WriteVersion(TGraph::IsA());
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b << fNpoints;
b.WriteFastArray(fX,fNpoints);
b.WriteFastArray(fY,fNpoints);
b << fFunctions;
b << (TObject *)fHistogram;
b << fMinimum;
b << fMaximum;
}
}
//______________________________________________________________________________
void TGraph::Zero(Int_t &k,Float_t AZ,Float_t BZ,Float_t E2,Float_t &X,Float_t &Y
,Int_t maxiterations)
{
//*-*-*-*-*-*-*-*-*-*-*-*Find zero of a continuous function*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// Underlaying routine for PaintGraph
// This function finds a real zero of the continuous real
// function Y(X) in a given interval (A,B). See accompanying
// notes for details of the argument list and calling sequence
//
//
static Float_t A, B, YA, ytest, Y1, X1, H;
static Int_t J1, IT, J3, J2;
Float_t YB, X2;
YB = 0;
//*-*______________________________________
//*-*- Calculate Y(X) at X=AZ.
if (k <= 0) {
A = AZ;
B = BZ;
X = A;
J1 = 1;
IT = 1;
k = J1;
return;
}
//*-*- Test whether Y(X) is sufficiently small.
if (TMath::Abs(Y) <= E2) { k = 2; return; }
//*-*- Calculate Y(X) at X=BZ.
if (J1 == 1) {
YA = Y;
X = B;
J1 = 2;
return;
}
//*-*- Test whether the signs of Y(AZ) and Y(BZ) are different.
//*-*- if not, begin the binary subdivision.
if (J1 != 2) goto L100;
if (YA*Y < 0) goto L120;
X1 = A;
Y1 = YA;
J1 = 3;
H = B - A;
J2 = 1;
X2 = A + 0.5*H;
J3 = 1;
IT++; //*-*- Check whether (maxiterations) function values have been calculated.
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Test whether a bracket has been found .
//*-*- If not,continue the search
L100:
if (J1 > 3) goto L170;
if (YA*Y >= 0) {
if (J3 >= J2) {
H = 0.5*H; J2 = 2*J2;
A = X1; YA = Y1; X2 = A + 0.5*H; J3 = 1;
}
else {
A = X; YA = Y; X2 = X + H; J3++;
}
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- The first bracket has been found.calculate the next X by the
//*-*- secant method based on the bracket.
L120:
B = X;
YB = Y;
J1 = 4;
L130:
if (TMath::Abs(YA) > TMath::Abs(YB)) { X1 = A; Y1 = YA; X = B; Y = YB; }
else { X1 = B; Y1 = YB; X = A; Y = YA; }
//*-*- Use the secant method based on the function values Y1 and Y.
//*-*- check that X2 is inside the interval (A,B).
L150:
X2 = X-Y*(X-X1)/(Y-Y1);
X1 = X;
Y1 = Y;
ytest = 0.5*TMath::Min(TMath::Abs(YA),TMath::Abs(YB));
if ((X2-A)*(X2-B) < 0) {
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- Calculate the next value of X by bisection . Check whether
//*-*- the maximum accuracy has been achieved.
L160:
X2 = 0.5*(A+B);
ytest = 0;
if ((X2-A)*(X2-B) >= 0) { k = 2; return; }
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Revise the bracket (A,B).
L170:
if (J1 != 4) return;
if (YA*Y < 0) { B = X; YB = Y; }
else { A = X; YA = Y; }
//*-*- Use ytest to decide the method for the next value of X.
if (ytest <= 0) goto L130;
if (TMath::Abs(Y)-ytest <= 0) goto L150;
goto L160;
}
*/
//
//
//______________________________________________________________________________
TGraph::TGraph(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =========================
fNpoints = 0;
fX = 0;
fY = 0;
fFunctions = 0;
fHistogram = 0;
fMaximum = -1111;
fMinimum = -1111;
}
//______________________________________________________________________________
TGraph::TGraph(Int_t n, Float_t *x, Float_t *y)
: TNamed("Graph","Graph"), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph normal constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
if (n <= 0) {
Error("TGraph", "illegal number of points (%d)", n);
return;
}
fFunctions = new TList(this);
fHistogram = 0;
fNpoints = n;
fX = new Float_t[n];
fY = new Float_t[n];
fMaximum = -1111;
fMinimum = -1111;
if (!x || !y) return;
for (Int_t i=0;i<n;i++) {
fX[i] = x[i];
fY[i] = y[i];
}
SetBit(kClipFrame);
}
//______________________________________________________________________________
TGraph::~TGraph()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default destructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =======================
delete [] fX;
delete [] fY;
if (!fFunctions) return;
fFunctions->Delete();
delete fFunctions;
fFunctions = 0;
delete fHistogram;
fHistogram = 0;
}
//______________________________________________________________________________
void TGraph::ComputeRange(Float_t &, Float_t &, Float_t &, Float_t &)
{
// this function is dummy in TGraph, but redefined by TGraphErrors
}
//______________________________________________________________________________
void TGraph::Draw(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ==========================================
//
// Options to draw a graph are described in TGraph::PaintGraph
char chopt[8] = " ";
if (strlen(option) < 7) strcpy(chopt,option);
else strncpy(chopt,option,7);
// in case of option *, set marker style to 3 (star) and replace
// * option by option P.
char *cstar = strchr(chopt,'*');
if (cstar) {
SetMarkerStyle(3);
cstar[0] = 'P';
}
AppendPad(chopt);
}
//______________________________________________________________________________
Int_t TGraph::DistancetoPrimitive(Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a graph*-*-*-*-*-*
//*-* ===========================================
// Compute the closest distance of approach from point px,py to this line.
// The distance is computed in pixels units.
//
//*-*- Are we on the axis?
Int_t distance;
if (fHistogram) {
distance = fHistogram->DistancetoPrimitive(px,py);
if (distance <= 0) return distance;
}
//*-*- Somewhere on the graph points?
const Int_t big = 9999;
const Int_t kMaxDiff = 10;
Int_t puxmin = gPad->XtoAbsPixel(gPad->GetUxmin());
Int_t puymin = gPad->YtoAbsPixel(gPad->GetUymin());
Int_t puxmax = gPad->XtoAbsPixel(gPad->GetUxmax());
Int_t puymax = gPad->YtoAbsPixel(gPad->GetUymax());
//*-*- return if point is not in the histogram area
if (px <= puxmin) return big;
if (py >= puymin) return big;
if (px >= puxmax) return big;
if (py <= puymax) return big;
//*-*- check if point is near one of the graph points
Int_t i, pxp, pyp, d;
distance = big;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < distance) distance = d;
}
if (distance < kMaxDiff) return distance;
for (i=0;i<fNpoints-1;i++) {
d = DistancetoLine(px, py, gPad->XtoPad(fX[i]), gPad->YtoPad(fY[i]), gPad->XtoPad(fX[i+1]), gPad->YtoPad(fY[i+1]));
if (d < distance) distance = d;
}
//*-*- Loop on the list of associated functions and user objects
TObject *f;
TIter next(fFunctions);
while ((f = (TObject*) next())) {
Int_t dist = f->DistancetoPrimitive(px,py);
if (dist < kMaxDiff) {gPad->SetSelected(f); return dist;}
}
return distance;
}
//______________________________________________________________________________
void TGraph::DrawGraph(Int_t n, Float_t *x, Float_t *y, Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with new attributes*-*-*-*-*-*-*-*-*-*
//*-* ===================================
TGraph *newgraph = new TGraph(n, x, y);
TAttLine::Copy(*newgraph);
TAttFill::Copy(*newgraph);
TAttMarker::Copy(*newgraph);
newgraph->SetBit(kCanDelete);
newgraph->AppendPad(option);
}
//______________________________________________________________________________
void TGraph::DrawPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph drawing options*-*-*-*-*-*
//*-* ==============================================
//
printf("TGraph::DrawPanel: not yet implementedn");
}
//______________________________________________________________________________
void TGraph::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
//*-* =========================================
// This member function is called when a graph is clicked with the locator
//
// If Left button clicked on one of the line end points, this point
// follows the cursor until button is released.
//
// if Middle button clicked, the line is moved parallel to itself
// until the button is released.
//
Int_t i, d;
Float_t xmin, xmax, ymin, ymax, dx, dy, dxr, dyr;
const Int_t kMaxDiff = 10;
static Bool_t MIDDLE;
static Int_t ipoint, pxp, pyp;
static Int_t px1,px2,py1,py2;
static Int_t pxold, pyold, px1old, py1old, px2old, py2old;
static Int_t dpx, dpy;
static Int_t *x=0, *y=0;
switch (event) {
case kButton1Down:
gGXW->SetLineColor(-1);
TAttLine::Modify(); //Change line attributes only if necessary
px1 = gPad->XtoAbsPixel(gPad->GetX1());
py1 = gPad->YtoAbsPixel(gPad->GetY1());
px2 = gPad->XtoAbsPixel(gPad->GetX2());
py2 = gPad->YtoAbsPixel(gPad->GetY2());
ipoint = -1;
if (x || y) break;
x = new Int_t[fNpoints+1];
y = new Int_t[fNpoints+1];
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
x[i] = pxp;
y[i] = pyp;
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) ipoint =i;
}
dpx = 0;
dpy = 0;
pxold = px;
pyold = py;
if (ipoint < 0) return;
if (ipoint == 0) {
px1old = 0;
py1old = 0;
px2old = gPad->XtoAbsPixel(fX[1]);
py2old = gPad->YtoAbsPixel(fY[1]);
} else if (ipoint == fNpoints-1) {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[fNpoints-2]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[fNpoints-2]));
px2old = 0;
py2old = 0;
} else {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint-1]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint-1]));
px2old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint+1]));
py2old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint+1]));
}
pxold = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint]));
pyold = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint]));
break;
case kMouseMotion:
MIDDLE = kTRUE;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) MIDDLE = kFALSE;
}
//*-*- check if point is close to an axis
if (MIDDLE) gPad->SetCursor(kMove);
else gPad->SetCursor(kHand);
break;
case kButton1Motion:
if (MIDDLE) {
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
dpx += px - pxold;
dpy += py - pyold;
pxold = px;
pyold = py;
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
} else {
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
pxold = px;
pxold = TMath::Max(pxold, px1);
pxold = TMath::Min(pxold, px2);
pyold = py;
pyold = TMath::Max(pyold, py2);
pyold = TMath::Min(pyold, py1);
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
}
break;
case kButton1Up:
//*-*- Compute x,y range
xmin = gPad->GetUxmin();
xmax = gPad->GetUxmax();
ymin = gPad->GetUymin();
ymax = gPad->GetUymax();
dx = xmax-xmin;
dy = ymax-ymin;
dxr = dx/(1 - gPad->GetLeftMargin() - gPad->GetRightMargin());
dyr = dy/(1 - gPad->GetBottomMargin() - gPad->GetTopMargin());
// Range() could change the size of the pad pixmap and therefore should
// be called before the other paint routines
gPad->Range(xmin - dxr*gPad->GetLeftMargin(),
ymin - dyr*gPad->GetBottomMargin(),
xmax + dxr*gPad->GetRightMargin(),
ymax + dyr*gPad->GetTopMargin());
gPad->RangeAxis(xmin, ymin, xmax, ymax);
if (MIDDLE) {
for(i=0;i<fNpoints;i++) {
fX[i] = gPad->PadtoX(gPad->AbsPixeltoX(x[i]+dpx));
fY[i] = gPad->PadtoY(gPad->AbsPixeltoY(y[i]+dpy));
}
} else {
fX[ipoint] = gPad->PadtoX(gPad->AbsPixeltoX(pxold));
fY[ipoint] = gPad->PadtoY(gPad->AbsPixeltoY(pyold));
}
delete [] x; x = 0;
delete [] y; y = 0;
gPad->Modified(kTRUE);
gGXW->SetLineColor(-1);
}
}
//______________________________________________________________________________
void TGraph::Fit(Text_t *fname, Option_t *option, Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Fit this graph with function fname*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// fname is the name of an already predefined function created by TF1
// Predefined functions such as Gaus, Expo and Poln are automatically
// created by ROOT.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TGraph::Paint for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your graph
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// graph->Fit("f1","R");
//
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,0.1,-8,100);
// func->SetParLimits(4,-10,-4);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->3 can vary freely
// Parameter 4 has boundaries [-10,-4] with initial value -8
// Parameter 5 is fixed to 100.
//
Int_t i, ierf, npar,nvpar,nparx,icstat;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,edm,errdef,werr;
TF1 *fnew1;
Double_t *arglist = new Double_t[100];
// Decode string choptin and fill Foption structure
Foption.Quiet = 0;
Foption.Verbose = 0;
Foption.Bound = 0;
Foption.Like = 0;
Foption.W1 = 0;
Foption.Errors = 0;
Foption.Range = 0;
Foption.Gradient= 0;
Foption.Nograph = 0;
Foption.Nostore = 0;
Foption.Plus = 0;
TString opt = option;
opt.ToUpper();
if (opt.Contains("Q")) Foption.Quiet = 1;
if (opt.Contains("V")){Foption.Verbose = 1; Foption.Quiet = 0;}
if (opt.Contains("W")) Foption.W1 = 1;
if (opt.Contains("E")) Foption.Errors = 1;
if (opt.Contains("R")) Foption.Range = 1;
if (opt.Contains("N")) Foption.Nostore = 1;
if (opt.Contains("0")) Foption.Nograph = 1;
if (opt.Contains("+")) Foption.Plus = 1;
xmin = fX[0];
xmax = fX[fNpoints-1];
ymin = fY[0];
ymax = fY[fNpoints-1];
for (i=0;i<fNpoints;i++) {
if (fX[i] < xmin) xmin = fX[i];
if (fX[i] > xmax) xmax = fX[i];
if (fY[i] < ymin) ymin = fY[i];
if (fY[i] > ymax) ymax = fY[i];
}
//*-*- Check if Minuit is initialized and create special functions
if (!gMinuit) gMinuit = new TMinuit(25);
if (!gROOT->GetFunction("gaus")) {
gF1 = new TF1("gaus","gaus",xmin,xmax);
gF1 = new TF1("expo","expo",xmin,xmax);
for (i=0;i<10;i++) gF1 = new TF1(Form("pol%d",i),Form("pol%d",i),xmin,xmax);
}
gMinuit->mncler();
gMinuit->SetObjectFit(this);
//*-*- Get pointer to the function by searching in the list of functions in ROOT
gF1 = gROOT->GetFunction(fname);
if (!gF1) { Printf("Unknown function: %s",fname); return; }
npar = gF1->GetNpar();
if (npar <=0) { Printf("Illegal number of parameters = %d",npar); return; }
//*-*- Check that function has same dimension as histogram
if (gF1->GetNdim() > 1) {
Printf("Error function %s is not 1-D",fname); return; }
//*-*- Is a Fit range specified?
if (Foption.Range) {
gF1->GetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
} else {
gF1->SetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
}
//*-*- If case of a predefined function, then compute initial values of parameters
Int_t special = gF1->GetNumber();
if (special == 100) InitGaus();
else if (special == 200) InitExpo();
else if (special == 299+npar) InitPolynom();
//*-*- Set error criterion for chisquare
arglist[0] = 1;
gMinuit->SetFCN(GraphFitChisquare);
gMinuit->mnexcm("SET ERR",arglist,1,ierf);
//*-*- Some initialisations
if (!Foption.Verbose) {
arglist[0] = -1;
gMinuit->mnexcm("SET PRINT", arglist,1,ierf);
arglist[0] = 0;
gMinuit->mnexcm("SET NOW", arglist,0,ierf);
}
//*-*- Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = gF1->GetParameter(i);
gF1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.3*TMath::Abs(par);
if (we <= TMath::Abs(par)*1e-6) we = 1;
gMinuit->mnparm(i,gF1->GetParName(i),par,we,al,bl,ierf);
}
if(nfixed > 0)gMinuit->mnexcm("FIX",arglist,nfixed,ierf); // Otto
//*-*- Reset Print level
if (!Foption.Quiet) {
if (Foption.Verbose) { arglist[0] = 2; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
else { arglist[0] = 0; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
}
//*-*- Perform minimization
SetBit(kFitInit);
arglist[0] = 5000; //MaxIterations
arglist[1] = 1e-2; //epsilon
gMinuit->mnexcm("MIGRAD",arglist,2,ierf);
if (Foption.Errors) {
gMinuit->mnexcm("HESSE",arglist,0,ierf);
gMinuit->mnexcm("MINOS",arglist,0,ierf);
}
//*-*- Get return status
for (i=0;i<npar;i++) {
gMinuit->mnpout(i,gF1->GetParName(i), par,we,al,bl,ierf);
if (Foption.Errors) werr = we;
else {
gMinuit->mnerrs(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
gF1->SetParameter(i,par);
gF1->SetParError(i,werr);
}
gMinuit->mnstat(amin,edm,errdef,nvpar,nparx,icstat);
gF1->SetChisquare(amin);
//*-*- Print final values of parameters.
if (!Foption.Quiet) {
if (Foption.Errors) gMinuit->mnprin(4,amin);
else gMinuit->mnprin(3,amin);
}
delete [] arglist;
//*-*- Store fitted function in histogram functions list and draw
if (!Foption.Nostore) {
if (!Foption.Plus) fFunctions->Delete();
fnew1 = new TF1();
gF1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax);
if (TestBit(kCanDelete)) return;
if (gPad) gPad->Modified();
}
}
//______________________________________________________________________________
void TGraph::FitPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph fit options*-*-*-*-*-*
//*-* ==========================================
//
// See class TFitPanel for example
if (gPad) {
gROOT->SetSelectedPrimitive(gPad->GetSelected());
gROOT->SetSelectedPad(gPad->GetSelectedPad());
}
TList *lc = (TList*)gROOT->GetListOfCanvases();
if (!lc->FindObject("fitpanelgraph")) {
char cmd[] = "TFitPanelGraph *fitpanel = new TFitPanelGraph("fitpanelgraph","Fit Panel",300,400);";
gInterpreter->ProcessLine(cmd);
return;
}
char cmdupd[] = "fitpanelgraph->SetDefaults(); fitpanelgraph->Show();";
gInterpreter->ProcessLine(cmdupd);
}
//______________________________________________________________________________
Float_t TGraph::GetErrorX(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
Float_t TGraph::GetErrorY(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
TH1F *TGraph::GetHistogram()
{
// Returns a pointer to the histogram used to draw the axis
// Takes into account the two following cases.
// 1- option 'A' was specified in TGraph::Draw. Return fHistogram
// 2- user had called TPad::DrawFrame. return pointer to hframe histogram
if (fHistogram) return fHistogram;
if (!gPad) return 0;
gPad->Modified();
gPad->Update();
if (fHistogram) return fHistogram;
TH1F *h1 = (TH1F*)gPad->GetPrimitive("hframe");
return h1;
}
//______________________________________________________________________________
void TGraph::GetPoint(Int_t i, Float_t &x, Float_t &y)
{
//*-*-*-*-*-*-*-*-*-*-*Get x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0 || i >= fNpoints) return;
if (!fX || !fY) return;
x = fX[i];
y = fY[i];
}
//______________________________________________________________________________
TAxis *TGraph::GetXaxis()
{
// Get x axis of the graph.
if (fHistogram) return fHistogram->GetXaxis();
return 0;
}
//______________________________________________________________________________
TAxis *TGraph::GetYaxis()
{
// Get y axis of the graph.
if (fHistogram) return fHistogram->GetYaxis();
return 0;
}
//______________________________________________________________________________
void GraphFitChisquare(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag)
{
//*-*-*-*-*-*Minimization function for Graphs using a Chisquare method*-*-*-*-*
//*-* =========================================================
Double_t cu,eu,fu,fsum;
Double_t dersum[25], grad[25];
static Double_t eysum[50];
Double_t x[1];
Float_t errormax;
Int_t bin, k, npfits, nparts, part;
TGraph *gr = (TGraph*)gMinuit->GetObjectFit();
Int_t n = gr->GetN();
Float_t *gx = gr->GetX();
Float_t *gy = gr->GetY();
npar = gF1->GetNpar();
Float_t cumin = gy[0];
Float_t cumax = gy[0];
if (flag == 2) for (k=0;k<npar;k++) dersum[k] = gin[k] = 0;
nparts = n/3;
if (nparts == 0) nparts = 1;
if (nparts > 40) nparts = 40;
Float_t fxmin = gF1->GetXmin();
Float_t fxmax = gF1->GetXmax();
Float_t dfx = (fxmax - fxmin)/nparts;
if (gr->TestBit(kFitInit)) {
for (part=0;part<nparts;part++) { eysum[part] = 0;}
}
gF1->InitArgs(x,u);
npfits = 0;
f = 0;
for (bin=0;bin<n;bin++) {
x[0] = gx[bin];
if (Foption.Range) {
if (x[0] < fxmin) continue;
if (x[0] > fxmax) continue;
}
cu = gy[bin];
fu = gF1->EvalPar(x,u);
eu = gr->GetErrorY(bin);
if (Foption.W1) eu = 1;
if (eu < 0) {
part = Int_t((x[0] - fxmin)/dfx);
if (part < 0) part = 0;
if (part >= nparts) part = nparts-1;
if (gr->TestBit(kFitInit)) {
eysum[part] += (cu-fu)*(cu-fu);
if (cu < cumin) cumin = cu;
if (cu > cumax) cumax = cu;
} else {
eu = eysum[part];
}
}
if (flag == 2) {
for (k=0;k<npar;k++) dersum[k] += 1; //should be the derivative
}
npfits++;
if (flag == 2) {
for (k=0;k<npar;k++) grad[k] += dersum[k]*(fu-cu)/eu; dersum[k] = 0;
}
if (eu) fsum = (cu-fu)/eu;
else fsum = cu-fu;
f += fsum*fsum;
}
// make a better error estimate to be used in the next iterations
if (gr->TestBit(kFitInit)) {
gr->ResetBit(kFitInit);
errormax = 0.2*(cumax-cumin);
for (part=0;part<nparts;part++) {
eysum[part] = TMath::Sqrt(eysum[part]);
if (eysum[part] > errormax) eysum[part] = errormax;
if (errormax < 0.2) eysum[part] = 1;
}
}
gF1->SetNumberFitPoints(npfits);
}
//______________________________________________________________________________
void TGraph::InitGaus()
{
//*-*-*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
//*-* ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
static Double_t sqrtpi = 2.506628;
//*-*- Compute mean value and RMS of the graph in the given range
allcha = sumx = sumx2 = 0;
for (bin=0;bin<fNpoints;bin++) {
x = fX[bin];
val = fY[bin];
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
Float_t binwidx = TMath::Abs((fX[fNpoints-1] - fX[0])/fNpoints);
if (rms == 0) rms = 1;
gF1->SetParameter(0,binwidx*allcha/(sqrtpi*rms));
gF1->SetParameter(1,mean);
gF1->SetParameter(2,rms);
}
//______________________________________________________________________________
void TGraph::InitExpo()
{
//*-*-*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
//*-* =======================================================
Double_t constant, slope;
Int_t ifail;
Int_t nchanx = xlast - xfirst + 1;
LeastSquareLinearFit(-nchanx, constant, slope, ifail);
gF1->SetParameter(0,constant);
gF1->SetParameter(1,slope);
}
//______________________________________________________________________________
void TGraph::InitPolynom()
{
//*-*-*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
//*-* ===================================================
Double_t fitpar[25];
Int_t nchanx = xlast - xfirst + 1;
Int_t npar = gF1->GetNpar();
LeastSquareFit( nchanx, npar, fitpar);
for (Int_t i=0;i<npar;i++) gF1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void TGraph::LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
//*-*-*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
//*-* =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
//
static Double_t zero = 0.;
static Double_t one = 1.;
static Int_t idim = 20;
static Double_t b[400] /* was [20][20] */;
static Int_t i, k, l, ifail;
static Double_t power;
static Double_t da[20], xk, yk;
if (m <= 2) {
LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Float_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
for (k = 0; k < fNpoints; ++k) {
xk = fX[k];
yk = fY[k];
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
if (ifail < 0) {
a[0] = fY[0];
for (i=1; i<m; ++i) a[i] = 0;
return;
}
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void TGraph::LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
//*-*-*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
//*-* =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
static Double_t xbar, ybar, x2bar;
static Int_t i, n;
static Double_t xybar;
static Float_t fn, xk, yk;
static Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
for (i = 0; i < fNpoints; ++i) {
xk = fX[i];
yk = fY[i];
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Float_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void TGraph::Paint(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ===========================================
if (strstr(option,"H") || strstr(option,"h")) {
PaintGrapHist(fNpoints, fX, fY, option);
} else {
PaintGraph(fNpoints, fX, fY, option);
}
TObject *f;
if (fFunctions) {
TIter next(fFunctions);
while ((f = (TObject*) next())) {
if (f->IsA() == TF1::Class()) f->Paint("lsame");
else f->Paint();
}
}
}
//______________________________________________________________________________
void TGraph::PaintGraph(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Control function to draw a graph*-*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or X(2) : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or Y(2) : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='F' : A fill area is drawn ('CF' draw a smooth fill area)
//
// chopt='A' : Axis are drawn around the graph
//
// chopt='C' : A smooth Curve is drawn
//
// chopt='*' : A Star is plotted at each point
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart is drawn at each point
//
// chopt='1' : ylow=rwymin
//
//
Int_t OptionLine , OptionAxis , OptionCurve,OptionStar ,OptionMark;
Int_t OptionBar , OptionR , OptionOne;
Int_t OptionFill , OptionZ ,OptionCurveFill;
Int_t i, npt, nloop;
Int_t drawtype;
Float_t xlow, xhigh, ylow, yhigh;
Float_t barxmin, barxmax, barymin, barymax;
Float_t uxmin, uxmax;
Float_t x1, xn, y1, yn;
Float_t dbar, bdelta;
//*-* ______________________________________
if (npoints <= 0) {
Error("PaintGraph", "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("R")) OptionR = 1; else OptionR = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
OptionZ = 0;
//*-* If no "drawing" option is selected and if chopt<>' '
//*-* nothing is done.
if (OptionLine+OptionFill+OptionCurve+OptionStar+OptionMark+OptionBar == 0) {
if (strlen(chopt) == 0) OptionLine=1;
else return;
}
if (OptionStar) SetMarkerStyle(3);
OptionCurveFill = 0;
if (OptionCurve && OptionFill) {
OptionCurveFill = 1;
OptionFill = 0;
}
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- Draw the Axis with a fixed number of division: 510
Float_t rwxmin,rwxmax, rwymin, rwymax, maximum, minimum;
if (OptionAxis) {
rwxmin = rwxmax = x[0];
rwymin = rwymax = y[0];
for (i=1;i<npoints;i++) {
if (x[i] < rwxmin) rwxmin = x[i];
if (x[i] > rwxmax) rwxmax = x[i];
if (y[i] < rwymin) rwymin = y[i];
if (y[i] > rwymax) rwymax = y[i];
}
ComputeRange(rwxmin, rwymin, rwxmax, rwymax); //this is redefined in TGraphErrors
if (rwxmin == rwxmax) rwxmax += 1.;
if (rwymin == rwymax) rwymax += 1.;
Float_t dx = 0.1*(rwxmax-rwxmin);
Float_t dy = 0.1*(rwymax-rwymin);
uxmin = rwxmin - dx;
uxmax = rwxmax + dx;
minimum = rwymin - dy;
maximum = rwymax + dy;
if (fMinimum != -1111) rwymin = minimum = fMinimum;
if (fMaximum != -1111) rwymax = maximum = fMaximum;
if (uxmin < 0 && rwxmin >= 0) {
if (gPad->GetLogx()) uxmin = 0.9*rwxmin;
else uxmin = 0;
}
if (uxmax > 0 && rwxmax <= 0) {
if (gPad->GetLogx()) uxmax = 1.1*rwxmax;
else uxmax = 0;
}
if (minimum < 0 && rwymin >= 0) {
if(gPad->GetLogy()) minimum = 0.9*rwymin;
else minimum = 0;
}
if (maximum > 0 && rwymax <= 0) {
if(gPad->GetLogy()) maximum = 1.1*rwymax;
else maximum = 0;
}
if (minimum <= 0 && gPad->GetLogy()) minimum = 0.001*maximum;
if (uxmin <= 0 && gPad->GetLogx()) {
if (uxmax > 1000) uxmin = 1;
else uxmin = 0.001*uxmax;
}
rwxmin = uxmin;
rwxmax = uxmax;
rwymin = minimum;
rwymax = maximum;
if (fHistogram) {
fHistogram->SetMinimum(rwymin);
fHistogram->SetMaximum(rwymax);
fHistogram->GetXaxis()->SetLimits(rwxmin,rwxmax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
}
//*-*- Create a temporary histogram and fill each channel with the function value
if (!fHistogram) {
fHistogram = new TH1F((char*)GetName(),(char*)GetTitle(),40,rwxmin,rwxmax);
if (!fHistogram) return;
fHistogram->SetMinimum(rwymin);
fHistogram->SetBit(kNoStats);
fHistogram->SetMaximum(rwymax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
fHistogram->SetDirectory(0);
}
fHistogram->Paint();
}
TF1 *fit = 0;
if (fFunctions) fit = (TF1*)fFunctions->First();
if (fit) {
if (fHistogram) {
fHistogram->PaintStat(0,fit);
} else {
TH1F *hfit = new TH1F("___0","",2,0,1);
hfit->PaintStat(0,fit);
delete hfit;
}
}
rwxmin = gPad->GetUxmin();
rwxmax = gPad->GetUxmax();
rwymin = gPad->GetUymin();
rwymax = gPad->GetUymax();
uxmin = gPad->PadtoX(rwxmin);
uxmax = gPad->PadtoX(rwxmax);
if (fHistogram) {
maximum = fHistogram->GetMaximum();
minimum = fHistogram->GetMinimum();
} else {
maximum = gPad->PadtoY(rwymax);
minimum = gPad->PadtoY(rwymin);
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Draw the graph with a polyline or a fill area
if (OptionLine || OptionFill) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
nloop = npoints;
if (OptionFill && (xn != x1 || yn != y1)) nloop++;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == nloop) {
ComputeLogs(npt, OptionZ);
Int_t bord = gStyle->GetDrawBorder();
if (OptionR) {
if (OptionFill) {
gPad->PaintFillArea(npt,yworkl,xworkl);
if (bord) gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else {
if (OptionFill) {
gPad->PaintFillArea(npt,xworkl,yworkl);
if (bord) gPad->PaintPolyLine(npt,xworkl,yworkl);
}
else gPad->PaintPolyLine(npt,xworkl,yworkl);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
}
}
//*-*- Draw the graph with a smooth Curve. Smoothing via Smooth
if (OptionCurve) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
drawtype = 1;
nloop = npoints;
if (OptionCurveFill) {
drawtype += 1000;
if (xn != x1 || yn != y1) nloop++;
}
if (!OptionR) {
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (yworkl[npt-1] < rwymin || yworkl[npt-1] > rwymax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=0;i<nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype += 10;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (xworkl[npt-1] < rwxmin || xworkl[npt-1] > rwxmax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=1;i<=nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the graph with a '*' on every points
if (OptionStar) {
SetMarkerStyle(3);
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph with the current polymarker on
//*-*- every points
if (OptionMark) {
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph as a bar chart
if (OptionBar) {
if (!OptionR) {
barxmin = x[0];
barxmax = x[0];
for (i=1;i<npoints;i++) {
if (x[i] < barxmin) barxmin = x[i];
if (x[i] > barxmax) barxmax = x[i];
}
bdelta = (barxmax-barxmin)/float(npoints);
}
else {
barymin = y[0];
barymax = y[0];
for (i=1;i<npoints;i++) {
if (y[i] < barymin) barymin = y[i];
if (y[i] > barymax) barymax = y[i];
}
bdelta = (barymax-barymin)/float(npoints);
}
dbar = 0.5*bdelta*gStyle->GetBarWidth();
if (!OptionR) {
for (i=1;i<=npoints;i++) {
xlow = x[i-1] - dbar;
xhigh = x[i-1] + dbar;
yhigh = y[i-1];
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
if (yworkl[0] < gPad->GetUymin()) yworkl[0] = gPad->GetUymin();
if (yworkl[1] < gPad->GetUymin()) continue;
if (yworkl[1] > gPad->GetUymax()) yworkl[0] = gPad->GetUymax();
if (yworkl[0] > gPad->GetUymax()) continue;
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
else {
for (i=1;i<=npoints;i++) {
xhigh = x[i-1];
ylow = y[i-1] - dbar;
yhigh = y[i-1] + dbar;
xlow = TMath::Max((Float_t)0, gPad->GetUxmin());
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::PaintGrapHist(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*Control function to draw a graphistogram*-*-*-*-*-*-*-*-*-*
//*-* ========================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or x[1] : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or y[1] : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='R' : Graph is drawn horizontaly, parallel to X axis.
// (default is vertically, parallel to Y axis)
// If option R is selected the user must give:
// 2 values for Y (y[0]=YMIN and y[1]=YMAX)
// N values for X, one for each channel.
// Otherwise the user must give:
// N values for Y, one for each channel.
// 2 values for X (x[0]=XMIN and x[1]=XMAX)
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='H' : An Histogram with equidistant bins is drawn
// as a polyline.
//
// chopt='F' : An histogram with equidistant bins is drawn
// as a fill area. Contour is not drawn unless
// chopt='H' is also selected..
//
// chopt='N' : Non equidistant bins (default is equidistant)
// If N is the number of channels array X and Y
// must be dimensionned as follow:
// If option R is not selected (default) then
// the user must give:
// (N+1) values for X (limits of channels).
// N values for Y, one for each channel.
// Otherwise the user must give:
// (N+1) values for Y (limits of channels).
// N values for X, one for each channel.
//
// chopt='F1': Idem as 'F' except that fill area is no more
// reparted arround axis X=0 or Y=0 .
//
// chopt='C' : A smooth Curve is drawn.
//
// chopt='*' : A Star is plotted at the center of each bin.
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart with equidistant bins is drawn as fill
// areas (Contours are drawn).
//
//
static const char *where = "PaintGraphHist";
const Int_t NPMXFA= 99;
Int_t OptionLine , OptionAxis , OptionCurve, OptionStar , OptionMark;
Int_t OptionBar , OptionRot , OptionOne;
Int_t OptionFill , OptionZ;
Int_t OptionHist , OptionBins , OptionMarker;
Int_t i, j, npt;
Int_t drawtype, drawborder, drawbordersav;
Float_t xlow, xhigh, ylow, yhigh;
Float_t wmin, wmax;
Float_t dbar, offset, wminstep;
Float_t delta = 0;
Float_t ylast = 0;
Float_t xi, xi1, xj, xj1, yi1, yi, yj, yj1, xwmin, ywmin;
Int_t first, last, nbins;
Int_t fillarea;
static char choptaxis[10] = " ";
//*-* ______________________________________
if (npoints <= 0) {
Error(where, "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("H")) OptionHist = 1; else OptionHist = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("R")) OptionRot = 1; else OptionRot = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("N")) OptionBins = 1; else OptionBins = 0;
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- If necessary the adresses of the vectors are saved in
//*-*- a link area.
OptionZ = 1;
if (OptionStar) SetMarkerStyle(3);
first = 1;
last = npoints;
nbins = last - first + 1;
//*-*- Draw the Axis with a fixed number of division: 510
Float_t baroffset = gStyle->GetBarOffset();
Float_t barwidth = gStyle->GetBarWidth();
Float_t rwxmin = gPad->GetUxmin();
Float_t rwxmax = gPad->GetUxmax();
Float_t rwymin = gPad->GetUymin();
Float_t rwymax = gPad->GetUymax();
Float_t uxmin = gPad->PadtoX(rwxmin);
Float_t uxmax = gPad->PadtoX(rwxmax);
Float_t rounding = (uxmax-uxmin)*1.e-5;
drawborder = gStyle->GetDrawBorder();
if (OptionAxis) {
Int_t nx1, nx2, ndivx, ndivy, ndiv;
choptaxis[0] = 0;
Float_t rwmin = rwxmin;
Float_t rwmax = rwxmax;
ndivx = gStyle->GetNdivisions("X");
ndivy = gStyle->GetNdivisions("Y");
if (ndivx > 1000) {
nx2 = ndivx/100;
nx1 = TMath::Max(1, ndivx%100);
ndivx = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsWNDC());
}
ndiv =TMath::Abs(ndivx);
if (ndivx < 0) strcat(choptaxis, "N");
if (gPad->GetGridx()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogx()) {
rwmin = TMath::Power(10,rwxmin);
rwmax = TMath::Power(10,rwxmax);
strcat(choptaxis, "G");
}
TGaxis *axis = new TGaxis();
axis->SetLineColor(gStyle->GetAxisColor("X"));
axis->SetTextColor(gStyle->GetLabelColor("X"));
axis->SetTextFont(gStyle->GetLabelFont("X"));
axis->SetLabelSize(gStyle->GetLabelSize("X"));
axis->SetLabelOffset(gStyle->GetLabelOffset("X"));
axis->SetTickSize(gStyle->GetTickLength("X"));
axis->PaintAxis(rwxmin,rwymin,rwxmax,rwymin,rwmin,rwmax,ndiv,choptaxis);
choptaxis[0] = 0;
rwmin = rwymin;
rwmax = rwymax;
if (ndivy < 0) {
nx2 = ndivy/100;
nx1 = TMath::Max(1, ndivy%100);
ndivy = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsHNDC());
strcat(choptaxis, "N");
}
ndiv =TMath::Abs(ndivy);
if (gPad->GetGridy()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogy()) {
rwmin = TMath::Power(10,rwymin);
rwmax = TMath::Power(10,rwymax);
strcat(choptaxis,"G");
}
axis->SetLineColor(gStyle->GetAxisColor("Y"));
axis->SetTextColor(gStyle->GetLabelColor("Y"));
axis->SetTextFont(gStyle->GetLabelFont("Y"));
axis->SetLabelSize(gStyle->GetLabelSize("Y"));
axis->SetLabelOffset(gStyle->GetLabelOffset("Y"));
axis->SetTickSize(gStyle->GetTickLength("Y"));
axis->PaintAxis(rwxmin,rwymin,rwxmin,rwymax,rwmin,rwmax,ndiv,choptaxis);
delete axis;
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Min-Max scope
if (!OptionRot) {wmin = x[0]; wmax = x[1];}
else {wmin = y[0]; wmax = y[1];}
if (!OptionBins) delta = (wmax - wmin)/ float(nbins);
//*-*- Draw the histogram with a fill area
if (OptionFill && !OptionCurve) {
fillarea = kTRUE;
if (!OptionRot) {
xwork[0] = wmin;
if (!OptionOne) ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
else ywork[0] = gPad->GetUymin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((j-first+1)*delta);
}
else {
xj1 = x[j]; xj = x[j-1];
if (xj1 < xj) {
if (j != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j];
}
ywork[npt-1] = y[j-1];
ywork[npt] = y[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (j == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
xwork[0] = xwork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++) {
}
else {
ywork[0] = wmin;
if (!OptionOne) xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
else xwork[0] = gPad->GetUxmin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((j-first+1)*delta);
}
else {
yj1 = y[j]; yj = y[j-1];
if (yj1 < yj) {
if (j != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[j-1]; ywork[npt] = y[j];
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (j == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
ywork[0] = ywork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++)
}
}
//*-*- Draw a standard Histogram (default)
if ((OptionHist) || strlen(chopt) == 0) {
if (!OptionRot) {
xwork[0] = wmin;
// ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
ywork[0] = gPad->GetUymin();
ywmin = ywork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((i-first+1)*delta);
}
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i];
}
ywork[npt-1] = y[i-1];
ywork[npt] = y[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (i == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
else {
ywork[0] = wmin;
xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
xwmin = xwork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((i-first+1)*delta);
}
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1]; ywork[npt] = y[i];
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (i == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
}
//*-*- Draw the histogram with a smooth Curve. The computing
//*-*- of the smoothing is done by the routine IGRAP1
if (OptionCurve) {
if (!OptionFill) drawtype = 1;
else {
if (!OptionOne) drawtype = 2;
else drawtype = 3;
}
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
ComputeLogs(npt, OptionZ);
if ((yworkl[npt] < rwymin) || (yworkl[npt] > rwymax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype = drawtype+10;
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
ComputeLogs(npt, OptionZ);
if ((xworkl[npt] < uxmin) || (xworkl[npt] > uxmax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the histogram with a simple line
OptionMarker = 0;
if ((OptionStar) || (OptionMark))OptionMarker=1;
if ((OptionMarker) || (OptionLine)) {
wminstep = wmin + 0.5*delta;
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wminstep + (i-first)*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
if ((ywork[npt-1] < rwymin) || (ywork[npt-1] > rwymax)) {
if ((ywork[npt-1] < rwymin)) ywork[npt-1] = rwymin;
if ((ywork[npt-1] > rwymax)) ywork[npt-1] = rwymax;
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
else {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wminstep+(i-first)*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
if ((xwork[npt-1] < uxmin) || (xwork[npt-1] > uxmax)) {
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine != 0 && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
}
//*-*- Draw the histogram as a bar chart
if (OptionBar) {
if (!OptionBins) { offset = delta*baroffset; dbar = delta*barwidth; }
else {
if (!OptionRot) {
offset = (x[1]-x[0])*baroffset;
dbar = (x[1]-x[0])*barwidth;
} else {
offset = (y[1]-y[0])*baroffset;
dbar = (y[1]-y[0])*barwidth;
}
}
drawbordersav = drawborder;
gStyle->SetDrawBorder(1);
if (!OptionRot) {
xlow = wmin+offset;
xhigh = wmin+offset+dbar;
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
for (i=first; i<=last;i++) {
yhigh = y[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
if (!OptionBins) {
xlow = xlow+delta;
xhigh = xhigh+delta;
}
else {
if (i < last) {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
Error(where, "X must be in increasing order");
return;
}
offset = (x[i+1]-x[i])*baroffset;
dbar = (x[i+1]-x[i])*barwidth;
xlow = x[i] + offset;
xhigh = x[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
else {
ylow = wmin + offset;
yhigh = wmin + offset + dbar;
if (!OptionOne) xlow = TMath::Max((Float_t)0,gPad->GetUxmin());
else xlow = gPad->GetUxmin();
for (i=first; i<=last;i++) {
xhigh = x[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
gPad->PaintBox(xlow,ylow,xhigh,yhigh);
if (!OptionBins) {
ylow = ylow + delta;
yhigh = yhigh + delta;
}
else {
if (i < last) {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
Error(where, "Y must be in increasing order");
return;
}
offset = (y[i+1]-y[i])*baroffset;
dbar = (y[i+1]-y[i])*barwidth;
ylow = y[i] + offset;
yhigh = y[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
gStyle->SetDrawBorder(drawbordersav);
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::ComputeLogs(Int_t npoints, Int_t opt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Convert WC from Log scales*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==========================
//
// Take the LOG10 of xwork and ywork according to the value of Options
// and put it in xworkl and yworkl.
//
// npoints : Number of points in xwork and in ywork.
//
for (Int_t i=0;i<npoints;i++) {
xworkl[i] = xwork[i];
yworkl[i] = ywork[i];
if (gPad->GetLogx()) {
if (xworkl[i] > 0) xworkl[i] = TMath::Log10(xworkl[i]);
else xworkl[i] = gPad->GetX1();
}
if (!opt && gPad->GetLogy()) {
if (yworkl[i] > 0) yworkl[i] = TMath::Log10(yworkl[i]);
else yworkl[i] = gPad->GetY1();
}
// if (yworkl[i] > gPad->GetUymax()) yworkl[i] = gPad->GetUymax();
}
}
//______________________________________________________________________________
void TGraph::Print(Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Print graph values*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==================
for (Int_t i=0;i<fNpoints;i++) {
printf("x[%d]=%g, y[%d]=%gn",i,fX[i],i,fY[i]);
}
}
//______________________________________________________________________________
void TGraph::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
char quote = '"';
out<<" "<<endl;
if (gROOT->ClassSaved(TGraph::Class())) {
out<<" ";
} else {
out<<" TGraph *";
}
out<<"graph = new TGraph("<<fNpoints<<");"<<endl;
out<<" graph->SetName("<<quote<<GetName()<<quote<<");"<<endl;
out<<" graph->SetTitle("<<quote<<GetTitle()<<quote<<");"<<endl;
SaveFillAttributes(out,"graph",0,1001);
SaveLineAttributes(out,"graph",1,1,1);
SaveMarkerAttributes(out,"graph",1,1,1);
for (Int_t i=0;i<fNpoints;i++) {
out<<" graph->SetPoint("<<i<<","<<fX[i]<<","<<fY[i]<<");"<<endl;
}
out<<" graph->Draw("
<<quote<<option<<quote<<");"<<endl;
}
//______________________________________________________________________________
void TGraph::SetMaximum(Float_t maximum)
{
fMaximum = maximum;
if (fHistogram) fHistogram->SetMaximum(maximum);
}
//______________________________________________________________________________
void TGraph::SetMinimum(Float_t minimum)
{
fMinimum = minimum;
if (fHistogram) fHistogram->SetMinimum(minimum);
}
//______________________________________________________________________________
void TGraph::SetPoint(Int_t i, Float_t x, Float_t y)
{
//*-*-*-*-*-*-*-*-*-*-*Set x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0) return;
if (i >= fNpoints) {
// re-allocate the object
Float_t *savex = new Float_t[i+1];
Float_t *savey = new Float_t[i+1];
if (fNpoints > 0) {
memcpy(savex,fX,fNpoints*sizeof(Float_t));
memcpy(savey,fY,fNpoints*sizeof(Float_t));
}
if (fX) delete [] fX;
if (fY) delete [] fY;
fX = savex;
fY = savey;
fNpoints = i+1;
}
fX[i] = x;
fY[i] = y;
}
//______________________________________________________________________________
void TGraph::Smooth(Int_t npoints, Float_t *x, Float_t *y, Int_t drawtype)
{
//*-*-*-*-*-*-*-*-*-*-*-*Smooth a curve given by N points*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
// Underlaying routine for Draw based on the CERN GD3 routine TVIPTE
//
// Author - Marlow etc. Modified by - P. Ward Date - 3.10.1973
//
// This routine draws a smooth tangentially continuous curve through
// the sequence of data points P(I) I=1,N where P(I)=(X(I),Y(I))
// the curve is approximated by a polygonal arc of short vectors .
// the data points can represent open curves, P(1) != P(N) or closed
// curves P(2) == P(N) . If a tangential discontinuity at P(I) is
// required , then set P(I)=P(I+1) . loops are also allowed .
//
// Reference Marlow and Powell,Harwell report No.R.7092.1972
// MCCONALOGUE,Computer Journal VOL.13,NO4,NOV1970PP392 6
//
// _Input parameters:
//
// npoints : Number of data points.
// x : Abscissa
// y : Ordinate
//
//
// delta is the accuracy required in constructing the curve.
// if it is zero then the routine calculates a value other-
// wise it uses this value. (default is 0.0)
//
//
Int_t i, k, kp, km, NpointsMax, banksize, n2, npt;
Int_t maxiterations, finished;
Int_t jtype, ktype, closed;
Float_t sxmin, sxmax, symin, symax;
Float_t delta;
Float_t xorg, yorg;
Float_t ratio_signs, xratio, yratio;
Int_t flgic, flgis;
Int_t iw, loptx;
Float_t P1, P2, P3, P4, P5, P6;
Float_t W1, W2, W3;
Float_t A, B, C, R, S, T, Z;
Float_t CO, SO, CT, ST, CTU, STU, XNT;
Float_t DX1, DY1, DX2, DY2, DK1, DK2;
Float_t XO, YO, DX, DY, XT, YT;
Float_t XA, XB, YA, YB;
Float_t U1, U2, U3, TJ;
Float_t CC, ERR;
Float_t SB, STH;
Float_t wsign, tsquare, tcube;
C = T = CO = SO = CT = ST = CTU = STU = DX1 = DY1 = DX2 = DY2 = 0;
XT = YT = XA = XB = YA = YB = U1 = U2 = U3 = TJ = SB = 0;
//*-* ______________________________________
NpointsMax = npoints*10;
n2 = NpointsMax-2;
banksize = n2;
Float_t *qlx = new Float_t[NpointsMax];
Float_t *qly = new Float_t[NpointsMax];
if (!qlx || !qly) {
Error("Smooth", "not enough space in memory");
return;
}
//*-*- Decode the type of curve according to
//*-*- chopt of IGHIST.
//*-*- ('S', 'SA', 'SA1' ,'XS', 'XSA', or 'XSA1')
if (drawtype >= 1000) drawtype -= 1000;
loptx = kFALSE;
jtype = drawtype-10;
if (jtype > 0) { ktype = jtype; loptx = kTRUE; }
else ktype = drawtype;
Float_t ruxmin = gPad->GetUxmin();
Float_t ruymin = gPad->GetUymin();
if (ktype == 3) {
xorg = ruxmin;
yorg = ruymin;
} else {
xorg = TMath::Max((Float_t)0,ruxmin);
yorg = TMath::Max((Float_t)0,ruymin);
}
maxiterations = 20;
delta = 0.00055;
//*-*- Scale data to the range 0-ratio_signs in X, 0-1 in Y
//*-*- where ratio_signs is the ratio between the number of changes
//*-*- of sign in Y divided by the number of changes of sign in X
sxmin = x[0];
sxmax = x[0];
symin = y[0];
symax = y[0];
Float_t six = 1;
Float_t siy = 1;
for (i=1;i<npoints;i++) {
if (i > 1) {
if ((x[i]-x[i-1])*(x[i-1]-x[i-2]) < 0) six++;
if ((y[i]-y[i-1])*(y[i-1]-y[i-2]) < 0) siy++;
}
if (x[i] < sxmin) sxmin = x[i];
if (x[i] > sxmax) sxmax = x[i];
if (y[i] < symin) symin = y[i];
if (y[i] > symax) symax = y[i];
}
closed = 0;
Float_t dx1n = TMath::Abs(x[npoints-1]-x[0]);
Float_t dy1n = TMath::Abs(y[npoints-1]-y[0]);
if (dx1n < 0.01*(sxmax-sxmin) && dy1n < 0.01*(symax-symin)) closed = 1;
if (sxmin == sxmax) xratio = 1;
else {
if (six > 1) ratio_signs = siy/six;
else ratio_signs = 20;
xratio = ratio_signs/(sxmax-sxmin);
}
if (symin == symax) yratio = 1;
else yratio = 1/(symax-symin);
qlx[0] = x[0];
qly[0] = y[0];
for (i=0;i<npoints;i++) {
x[i] = (x[i]-sxmin)*xratio;
y[i] = (y[i]-symin)*yratio;
}
//*-*- finished is minus one if we must draw a straight line from P(k-1)
//*-*- to P(k). finished is one if the last call to IPL has < N2
//*-*- points. finished is zero otherwise. npt counts the X and Y
//*-*- coordinates in work . When npt=N2 a call to IPL is made.
finished = 0;
npt = 1;
k = 1;
//*-*- Convert coordinates back to original system
//*-*- Separate the set of data points into arcs P(k-1),P(k).
//*-*- Calculate the direction cosines. first consider whether
//*-*- there is a continuous tangent at the endpoints.
if (!closed) {
if (x[0] != x[npoints-1] || y[0] != y[npoints-1]) goto L40;
if (x[npoints-2] == x[npoints-1] && y[npoints-2] == y[npoints-1]) goto L40;
if (x[0] == x[1] && y[0] == y[1]) goto L40;
}
flgic = kFALSE;
flgis = kTRUE;
//*-*- flgic is true if the curve is open and false if it is closed.
//*-*- flgis is true in the main loop, but is false if there is
//*-*- a deviation from the main loop.
km = npoints - 1;
//*-*- Calculate direction cosines at P(1) using P(N-1),P(1),P(2).
goto L100;
L40:
flgic = kTRUE;
flgis = kFALSE;
//*-*- Skip excessive consecutive equal points.
L50:
if (k >= npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
k++;
if (x[k-1] == x[k-2] && y[k-1] == y[k-2]) goto L50;
L60:
km = k-1;
if (k > npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
if (k < npoints) goto L90;
if (!flgic) { kp = 2; goto L130;}
L80:
if (flgis) goto L150;
//*-*- Draw a straight line from P(k-1) to P(k).
finished = -1;
goto L170;
//*-*- Test whether P(k) is a cusp.
L90:
if (x[k-1] == x[k] && y[k-1] == y[k]) goto L80;
L100:
kp = k+1;
goto L130;
//*-*- Branch if the next section of the curve begins at a cusp.
L110:
if (!flgis) goto L50;
//*-*- Carry forward the direction cosines from the previous arc.
L120:
CO = CT;
SO = ST;
k++;
goto L60;
//*-*- Calculate the direction cosines at P(k). If k=1 then
//*-*- N-1 is used for k-1. If k=N then 2 is used for k+1.
//*-*- direction cosines at P(k) obtained from P(k-1),P(k),P(k+1).
L130:
DX1 = x[k-1] - x[km-1];
DY1 = y[k-1] - y[km-1];
DK1 = DX1*DX1 + DY1*DY1;
DX2 = x[kp-1] - x[k-1];
DY2 = y[kp-1] - y[k-1];
DK2 = DX2*DX2 + DY2*DY2;
CTU = DX1*DK2 + DX2*DK1;
STU = DY1*DK2 + DY2*DK1;
XNT = CTU*CTU + STU*STU;
//*-*- If both ctu and stu are zero,then default.This can
//*-*- occur when P(k)=P(k+1). I.E. A loop.
if (XNT < 1.E-25) {
CTU = DY1;
STU =-DX1;
XNT = DK1;
}
//*-*- Normalise direction cosines.
CT = CTU/TMath::Sqrt(XNT);
ST = STU/TMath::Sqrt(XNT);
if (flgis) goto L160;
//*-*- Direction cosines at P(k-1) obtained from P(k-1),P(k),P(k+1).
W3 = 2*(DX1*DY2-DX2*DY1);
CO = CTU+W3*DY1;
SO = STU-W3*DX1;
XNT = 1/TMath::Sqrt(CO*CO+SO*SO);
CO = CO*XNT;
SO = SO*XNT;
flgis = kTRUE;
goto L170;
//*-*- Direction cosines at P(k) obtained from P(k-2),P(k-1),P(k).
L150:
W3 = 2*(DX1*DY2-DX2*DY1);
CT = CTU-W3*DY2;
ST = STU+W3*DX2;
XNT = 1/TMath::Sqrt(CT*CT+ST*ST);
CT = CT*XNT;
ST = ST*XNT;
flgis = kFALSE;
goto L170;
L160:
if (k <= 1) goto L120;
//*-*- For the arc between P(k-1) and P(k) with direction cosines CO,
//*-*- SO and CT,ST respectively, calculate the coefficients of the
//*-*- parametric cubic represented by X(T) and Y(T) where
//*-*- X(T)=XA*T**3 + XB*T**2 + CO*T + XO
//*-*- Y(T)=YA*T**3 + YB*T**2 + SO*T + YO
L170:
XO = x[k-2];
YO = y[k-2];
DX = x[k-1] - XO;
DY = y[k-1] - YO;
//*-*- Initialise the values of X(TI),Y(TI) in XT and YT respectively.
XT = XO;
YT = YO;
if (finished < 0) { //*-*- Draw a straight line between (XO,YO) and (XT,YT)
XT += DX;
YT += DY;
goto L300;
}
C = DX*DX+DY*DY;
A = CO+CT;
B = SO+ST;
R = DX*A+DY*B;
T = C*6/(TMath::Sqrt(R*R+2*(7-CO*CT-SO*ST)*C)+R);
tsquare = T*T;
tcube = T*tsquare;
XA = (A*T-2*DX)/tcube;
XB = (3*DX-(CO+A)*T)/tsquare;
YA = (B*T-2*DY)/tcube;
YB = (3*DY-(SO+B)*T)/tsquare;
//*-*- If the curve is close to a straight line then use a straight
//*-*- line between (XO,YO) and (XT,YT).
if (.75*TMath::Max(TMath::Abs(DX*SO-DY*CO),TMath::Abs(DX*ST-DY*CT)) <= delta) {
finished = -1;
XT += DX;
YT += DY;
goto L300;
}
//*-*- Calculate a set of values 0 == T(0).LTCT(1) < ... < T(M)=TC
//*-*- such that polygonal arc joining X(T(J)),Y(T(J)) (J=0,1,..M)
//*-*- is within the required accuracy of the curve
TJ = 0;
U1 = YA*XB-YB*XA;
U2 = YB*CO-XB*SO;
U3 = SO*XA-YA*CO;
//*-*- Given T(J), calculate T(J+1). The values of X(T(J)),
//*-*- Y(T(J)) T(J) are contained in XT,YT and TJ respectively.
L180:
S = T - TJ;
iw = -2;
//*-*- Define iw here later.
P1 = (2*U1)*TJ-U3;
P2 = (U1*TJ-U3)*3*TJ+U2;
P3 = 3*TJ*YA+YB;
P4 = (P3+YB)*TJ+SO;
P5 = 3*TJ*XA+XB;
P6 = (P5+XB)*TJ+CO;
//*-*- Test D(TJ,THETA). A is set to (Y(TJ+S)-Y(TJ))/S.B is
//*-*- set to (X(TJ+S)-X(TJ))/S.
CC = 0.8209285;
ERR = 0.1209835;
L190:
iw -= 2;
L200:
A = (S*YA+P3)*S+P4;
B = (S*XA+P5)*S+P6;
//*-*- Set Z to PSI(D/delta)-CC.
W1 = -S*(S*U1+P1);
W2 = S*S*U1-P2;
W3 = 1.5*W1+W2;
//*-*- Set the estimate of (THETA-TJ)/S.Then set the numerator
//*-*- of the expression (EQUATION 4.4)/S. Then set the square
//*-*- of D(TJ,TJ+S)/delta. Then replace Z by PSI(D/delta)-CC.
if (W3 > 0) wsign = TMath::Abs(W1);
else wsign = -TMath::Abs(W1);
STH = 0.5+wsign/(3.4*TMath::Abs(W1)+5.2*TMath::Abs(W3));
Z = S*STH*(S-S*STH)*(W1*STH+W1+W2);
Z = Z*Z/((A*A+B*B)*(delta*delta));
Z = (Z+2.642937)*Z/((.3715652*Z+3.063444)*Z+.2441889)-CC;
//*-*- Branch if Z has been calculated
if (iw > 0) goto L250;
if (Z > ERR) goto L240;
goto L220;
L210:
iw -= 2;
L220:
if (iw+2 == 0) goto L190;
if (iw+2 > 0) goto L290;
//*-*- Last part of arc.
L230:
XT = x[k-1];
YT = y[k-1];
S = 0;
goto L300;
//*-*- Z(S). find a value of S where 0 <= S <= SB such that
//*-*- TMath::Abs(Z(S)) < ERR
L240:
kp = 0;
C = Z;
SB = S;
L250:
Zero(kp,0,SB,ERR,S,Z,maxiterations);
if (kp == 2) goto L210;
if (kp > 2) {
Error("Smooth", "Attempt to plot outside plot limits");
goto L230;
}
if (iw > 0) goto L200;
//*-*- Set Z=Z(S) for S=0.
if (iw < 0) {
Z = -CC;
iw = 0;
goto L250;
}
//*-*- Set Z=Z(S) for S=SB.
Z = C;
iw = 1;
goto L250;
//*-*- Update TJ,XT and YT.
L290:
XT = XT + S*B;
YT = YT + S*A;
TJ = S + TJ;
//*-*- Convert coordinates to original system
L300:
qlx[npt] = sxmin + XT/xratio;
qly[npt] = symin + YT/yratio;
npt++;
//*-*- If a fill area must be drawn and if the banks LX and
//*-*- LY are too small they are enlarged in order to draw
//*-*- the filled area in one go.
if (npt < banksize) goto L320;
if (drawtype >= 1000 || ktype > 1) {
Int_t newsize = banksize + n2;
Float_t *qtemp = new Float_t[banksize];
for (i=0;i<banksize;i++) qtemp[i] = qlx[i];
delete [] qlx;
qlx = new Float_t[newsize];
for (i=0;i<banksize;i++) qlx[i] = qtemp[i];
for (i=0;i<banksize;i++) qtemp[i] = qly[i];
delete [] qly;
qly = new Float_t[newsize];
for (i=0;i<banksize;i++) qly[i] = qtemp[i];
delete [] qtemp;
banksize = newsize;
goto L320;
}
//*-*- Draw the graph
L310:
if (drawtype >= 1000) {
gPad->PaintFillArea(npt,qlx,qly, "B");
}
else {
if (ktype > 1) {
if (!loptx) {
qlx[npt] = qlx[npt-1];
qlx[npt+1] = qlx[0];
qly[npt] = yorg;
qly[npt+1] = yorg;
}
else {
qlx[npt] = xorg;
qlx[npt+1] = xorg;
qly[npt] = qly[npt-1];
qly[npt+1] = qly[0];
}
gPad->PaintFillArea(npt+2,qlx,qly);
}
gPad->PaintPolyLine(npt,qlx,qly);
}
npt = 1;
qlx[0] = sxmin + XT/xratio;
qly[0] = symin + YT/yratio;
L320:
if (finished > 0) goto L390;
if (finished < 0) { finished = 0; goto L110;}
if (S > 0) goto L180;
goto L110;
//*-*- Convert coordinates back to original system
L390:
for (i=0;i<npoints;i++) {
x[i] = sxmin + x[i]/xratio;
y[i] = symin + y[i]/yratio;
}
delete [] qlx;
delete [] qly;
}
//______________________________________________________________________________
void TGraph::Streamer(TBuffer &b)
{
// Stream an object of class TGraph.
if (b.IsReading()) {
b.ReadVersion(); //Version_t v = b.ReadVersion();
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNpoints;
fX = new Float_t[fNpoints];
fY = new Float_t[fNpoints];
b.ReadFastArray(fX,fNpoints);
b.ReadFastArray(fY,fNpoints);
b >> fFunctions;
b >> fHistogram;
if (fHistogram) fHistogram->SetDirectory(0);
b >> fMinimum;
b >> fMaximum;
} else {
b.WriteVersion(TGraph::IsA());
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b << fNpoints;
b.WriteFastArray(fX,fNpoints);
b.WriteFastArray(fY,fNpoints);
b << fFunctions;
b << (TObject *)fHistogram;
b << fMinimum;
b << fMaximum;
}
}
//______________________________________________________________________________
void TGraph::Zero(Int_t &k,Float_t AZ,Float_t BZ,Float_t E2,Float_t &X,Float_t &Y
,Int_t maxiterations)
{
//*-*-*-*-*-*-*-*-*-*-*-*Find zero of a continuous function*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// Underlaying routine for PaintGraph
// This function finds a real zero of the continuous real
// function Y(X) in a given interval (A,B). See accompanying
// notes for details of the argument list and calling sequence
//
//
static Float_t A, B, YA, ytest, Y1, X1, H;
static Int_t J1, IT, J3, J2;
Float_t YB, X2;
YB = 0;
//*-*______________________________________
//*-*- Calculate Y(X) at X=AZ.
if (k <= 0) {
A = AZ;
B = BZ;
X = A;
J1 = 1;
IT = 1;
k = J1;
return;
}
//*-*- Test whether Y(X) is sufficiently small.
if (TMath::Abs(Y) <= E2) { k = 2; return; }
//*-*- Calculate Y(X) at X=BZ.
if (J1 == 1) {
YA = Y;
X = B;
J1 = 2;
return;
}
//*-*- Test whether the signs of Y(AZ) and Y(BZ) are different.
//*-*- if not, begin the binary subdivision.
if (J1 != 2) goto L100;
if (YA*Y < 0) goto L120;
X1 = A;
Y1 = YA;
J1 = 3;
H = B - A;
J2 = 1;
X2 = A + 0.5*H;
J3 = 1;
IT++; //*-*- Check whether (maxiterations) function values have been calculated.
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Test whether a bracket has been found .
//*-*- If not,continue the search
L100:
if (J1 > 3) goto L170;
if (YA*Y >= 0) {
if (J3 >= J2) {
H = 0.5*H; J2 = 2*J2;
A = X1; YA = Y1; X2 = A + 0.5*H; J3 = 1;
}
else {
A = X; YA = Y; X2 = X + H; J3++;
}
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- The first bracket has been found.calculate the next X by the
//*-*- secant method based on the bracket.
L120:
B = X;
YB = Y;
J1 = 4;
L130:
if (TMath::Abs(YA) > TMath::Abs(YB)) { X1 = A; Y1 = YA; X = B; Y = YB; }
else { X1 = B; Y1 = YB; X = A; Y = YA; }
//*-*- Use the secant method based on the function values Y1 and Y.
//*-*- check that X2 is inside the interval (A,B).
L150:
X2 = X-Y*(X-X1)/(Y-Y1);
X1 = X;
Y1 = Y;
ytest = 0.5*TMath::Min(TMath::Abs(YA),TMath::Abs(YB));
if ((X2-A)*(X2-B) < 0) {
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- Calculate the next value of X by bisection . Check whether
//*-*- the maximum accuracy has been achieved.
L160:
X2 = 0.5*(A+B);
ytest = 0;
if ((X2-A)*(X2-B) >= 0) { k = 2; return; }
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Revise the bracket (A,B).
L170:
if (J1 != 4) return;
if (YA*Y < 0) { B = X; YB = Y; }
else { A = X; YA = Y; }
//*-*- Use ytest to decide the method for the next value of X.
if (ytest <= 0) goto L130;
if (TMath::Abs(Y)-ytest <= 0) goto L150;
goto L160;
}
ROOT page - Class index - Top of the page
This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.
 */
//
//
//______________________________________________________________________________
TGraph::TGraph(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =========================
fNpoints = 0;
fX = 0;
fY = 0;
fFunctions = 0;
fHistogram = 0;
fMaximum = -1111;
fMinimum = -1111;
}
//______________________________________________________________________________
TGraph::TGraph(Int_t n, Float_t *x, Float_t *y)
: TNamed("Graph","Graph"), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph normal constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
if (n <= 0) {
Error("TGraph", "illegal number of points (%d)", n);
return;
}
fFunctions = new TList(this);
fHistogram = 0;
fNpoints = n;
fX = new Float_t[n];
fY = new Float_t[n];
fMaximum = -1111;
fMinimum = -1111;
if (!x || !y) return;
for (Int_t i=0;i<n;i++) {
fX[i] = x[i];
fY[i] = y[i];
}
SetBit(kClipFrame);
}
//______________________________________________________________________________
TGraph::~TGraph()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default destructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =======================
delete [] fX;
delete [] fY;
if (!fFunctions) return;
fFunctions->Delete();
delete fFunctions;
fFunctions = 0;
delete fHistogram;
fHistogram = 0;
}
//______________________________________________________________________________
void TGraph::ComputeRange(Float_t &, Float_t &, Float_t &, Float_t &)
{
// this function is dummy in TGraph, but redefined by TGraphErrors
}
//______________________________________________________________________________
void TGraph::Draw(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ==========================================
//
// Options to draw a graph are described in TGraph::PaintGraph
char chopt[8] = " ";
if (strlen(option) < 7) strcpy(chopt,option);
else strncpy(chopt,option,7);
// in case of option *, set marker style to 3 (star) and replace
// * option by option P.
char *cstar = strchr(chopt,'*');
if (cstar) {
SetMarkerStyle(3);
cstar[0] = 'P';
}
AppendPad(chopt);
}
//______________________________________________________________________________
Int_t TGraph::DistancetoPrimitive(Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a graph*-*-*-*-*-*
//*-* ===========================================
// Compute the closest distance of approach from point px,py to this line.
// The distance is computed in pixels units.
//
//*-*- Are we on the axis?
Int_t distance;
if (fHistogram) {
distance = fHistogram->DistancetoPrimitive(px,py);
if (distance <= 0) return distance;
}
//*-*- Somewhere on the graph points?
const Int_t big = 9999;
const Int_t kMaxDiff = 10;
Int_t puxmin = gPad->XtoAbsPixel(gPad->GetUxmin());
Int_t puymin = gPad->YtoAbsPixel(gPad->GetUymin());
Int_t puxmax = gPad->XtoAbsPixel(gPad->GetUxmax());
Int_t puymax = gPad->YtoAbsPixel(gPad->GetUymax());
//*-*- return if point is not in the histogram area
if (px <= puxmin) return big;
if (py >= puymin) return big;
if (px >= puxmax) return big;
if (py <= puymax) return big;
//*-*- check if point is near one of the graph points
Int_t i, pxp, pyp, d;
distance = big;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < distance) distance = d;
}
if (distance < kMaxDiff) return distance;
for (i=0;i<fNpoints-1;i++) {
d = DistancetoLine(px, py, gPad->XtoPad(fX[i]), gPad->YtoPad(fY[i]), gPad->XtoPad(fX[i+1]), gPad->YtoPad(fY[i+1]));
if (d < distance) distance = d;
}
//*-*- Loop on the list of associated functions and user objects
TObject *f;
TIter next(fFunctions);
while ((f = (TObject*) next())) {
Int_t dist = f->DistancetoPrimitive(px,py);
if (dist < kMaxDiff) {gPad->SetSelected(f); return dist;}
}
return distance;
}
//______________________________________________________________________________
void TGraph::DrawGraph(Int_t n, Float_t *x, Float_t *y, Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with new attributes*-*-*-*-*-*-*-*-*-*
//*-* ===================================
TGraph *newgraph = new TGraph(n, x, y);
TAttLine::Copy(*newgraph);
TAttFill::Copy(*newgraph);
TAttMarker::Copy(*newgraph);
newgraph->SetBit(kCanDelete);
newgraph->AppendPad(option);
}
//______________________________________________________________________________
void TGraph::DrawPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph drawing options*-*-*-*-*-*
//*-* ==============================================
//
printf("TGraph::DrawPanel: not yet implementedn");
}
//______________________________________________________________________________
void TGraph::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
//*-* =========================================
// This member function is called when a graph is clicked with the locator
//
// If Left button clicked on one of the line end points, this point
// follows the cursor until button is released.
//
// if Middle button clicked, the line is moved parallel to itself
// until the button is released.
//
Int_t i, d;
Float_t xmin, xmax, ymin, ymax, dx, dy, dxr, dyr;
const Int_t kMaxDiff = 10;
static Bool_t MIDDLE;
static Int_t ipoint, pxp, pyp;
static Int_t px1,px2,py1,py2;
static Int_t pxold, pyold, px1old, py1old, px2old, py2old;
static Int_t dpx, dpy;
static Int_t *x=0, *y=0;
switch (event) {
case kButton1Down:
gGXW->SetLineColor(-1);
TAttLine::Modify(); //Change line attributes only if necessary
px1 = gPad->XtoAbsPixel(gPad->GetX1());
py1 = gPad->YtoAbsPixel(gPad->GetY1());
px2 = gPad->XtoAbsPixel(gPad->GetX2());
py2 = gPad->YtoAbsPixel(gPad->GetY2());
ipoint = -1;
if (x || y) break;
x = new Int_t[fNpoints+1];
y = new Int_t[fNpoints+1];
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
x[i] = pxp;
y[i] = pyp;
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) ipoint =i;
}
dpx = 0;
dpy = 0;
pxold = px;
pyold = py;
if (ipoint < 0) return;
if (ipoint == 0) {
px1old = 0;
py1old = 0;
px2old = gPad->XtoAbsPixel(fX[1]);
py2old = gPad->YtoAbsPixel(fY[1]);
} else if (ipoint == fNpoints-1) {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[fNpoints-2]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[fNpoints-2]));
px2old = 0;
py2old = 0;
} else {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint-1]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint-1]));
px2old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint+1]));
py2old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint+1]));
}
pxold = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint]));
pyold = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint]));
break;
case kMouseMotion:
MIDDLE = kTRUE;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) MIDDLE = kFALSE;
}
//*-*- check if point is close to an axis
if (MIDDLE) gPad->SetCursor(kMove);
else gPad->SetCursor(kHand);
break;
case kButton1Motion:
if (MIDDLE) {
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
dpx += px - pxold;
dpy += py - pyold;
pxold = px;
pyold = py;
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
} else {
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
pxold = px;
pxold = TMath::Max(pxold, px1);
pxold = TMath::Min(pxold, px2);
pyold = py;
pyold = TMath::Max(pyold, py2);
pyold = TMath::Min(pyold, py1);
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
}
break;
case kButton1Up:
//*-*- Compute x,y range
xmin = gPad->GetUxmin();
xmax = gPad->GetUxmax();
ymin = gPad->GetUymin();
ymax = gPad->GetUymax();
dx = xmax-xmin;
dy = ymax-ymin;
dxr = dx/(1 - gPad->GetLeftMargin() - gPad->GetRightMargin());
dyr = dy/(1 - gPad->GetBottomMargin() - gPad->GetTopMargin());
// Range() could change the size of the pad pixmap and therefore should
// be called before the other paint routines
gPad->Range(xmin - dxr*gPad->GetLeftMargin(),
ymin - dyr*gPad->GetBottomMargin(),
xmax + dxr*gPad->GetRightMargin(),
ymax + dyr*gPad->GetTopMargin());
gPad->RangeAxis(xmin, ymin, xmax, ymax);
if (MIDDLE) {
for(i=0;i<fNpoints;i++) {
fX[i] = gPad->PadtoX(gPad->AbsPixeltoX(x[i]+dpx));
fY[i] = gPad->PadtoY(gPad->AbsPixeltoY(y[i]+dpy));
}
} else {
fX[ipoint] = gPad->PadtoX(gPad->AbsPixeltoX(pxold));
fY[ipoint] = gPad->PadtoY(gPad->AbsPixeltoY(pyold));
}
delete [] x; x = 0;
delete [] y; y = 0;
gPad->Modified(kTRUE);
gGXW->SetLineColor(-1);
}
}
//______________________________________________________________________________
void TGraph::Fit(Text_t *fname, Option_t *option, Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Fit this graph with function fname*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// fname is the name of an already predefined function created by TF1
// Predefined functions such as Gaus, Expo and Poln are automatically
// created by ROOT.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TGraph::Paint for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your graph
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// graph->Fit("f1","R");
//
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,0.1,-8,100);
// func->SetParLimits(4,-10,-4);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->3 can vary freely
// Parameter 4 has boundaries [-10,-4] with initial value -8
// Parameter 5 is fixed to 100.
//
Int_t i, ierf, npar,nvpar,nparx,icstat;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,edm,errdef,werr;
TF1 *fnew1;
Double_t *arglist = new Double_t[100];
// Decode string choptin and fill Foption structure
Foption.Quiet = 0;
Foption.Verbose = 0;
Foption.Bound = 0;
Foption.Like = 0;
Foption.W1 = 0;
Foption.Errors = 0;
Foption.Range = 0;
Foption.Gradient= 0;
Foption.Nograph = 0;
Foption.Nostore = 0;
Foption.Plus = 0;
TString opt = option;
opt.ToUpper();
if (opt.Contains("Q")) Foption.Quiet = 1;
if (opt.Contains("V")){Foption.Verbose = 1; Foption.Quiet = 0;}
if (opt.Contains("W")) Foption.W1 = 1;
if (opt.Contains("E")) Foption.Errors = 1;
if (opt.Contains("R")) Foption.Range = 1;
if (opt.Contains("N")) Foption.Nostore = 1;
if (opt.Contains("0")) Foption.Nograph = 1;
if (opt.Contains("+")) Foption.Plus = 1;
xmin = fX[0];
xmax = fX[fNpoints-1];
ymin = fY[0];
ymax = fY[fNpoints-1];
for (i=0;i<fNpoints;i++) {
if (fX[i] < xmin) xmin = fX[i];
if (fX[i] > xmax) xmax = fX[i];
if (fY[i] < ymin) ymin = fY[i];
if (fY[i] > ymax) ymax = fY[i];
}
//*-*- Check if Minuit is initialized and create special functions
if (!gMinuit) gMinuit = new TMinuit(25);
if (!gROOT->GetFunction("gaus")) {
gF1 = new TF1("gaus","gaus",xmin,xmax);
gF1 = new TF1("expo","expo",xmin,xmax);
for (i=0;i<10;i++) gF1 = new TF1(Form("pol%d",i),Form("pol%d",i),xmin,xmax);
}
gMinuit->mncler();
gMinuit->SetObjectFit(this);
//*-*- Get pointer to the function by searching in the list of functions in ROOT
gF1 = gROOT->GetFunction(fname);
if (!gF1) { Printf("Unknown function: %s",fname); return; }
npar = gF1->GetNpar();
if (npar <=0) { Printf("Illegal number of parameters = %d",npar); return; }
//*-*- Check that function has same dimension as histogram
if (gF1->GetNdim() > 1) {
Printf("Error function %s is not 1-D",fname); return; }
//*-*- Is a Fit range specified?
if (Foption.Range) {
gF1->GetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
} else {
gF1->SetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
}
//*-*- If case of a predefined function, then compute initial values of parameters
Int_t special = gF1->GetNumber();
if (special == 100) InitGaus();
else if (special == 200) InitExpo();
else if (special == 299+npar) InitPolynom();
//*-*- Set error criterion for chisquare
arglist[0] = 1;
gMinuit->SetFCN(GraphFitChisquare);
gMinuit->mnexcm("SET ERR",arglist,1,ierf);
//*-*- Some initialisations
if (!Foption.Verbose) {
arglist[0] = -1;
gMinuit->mnexcm("SET PRINT", arglist,1,ierf);
arglist[0] = 0;
gMinuit->mnexcm("SET NOW", arglist,0,ierf);
}
//*-*- Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = gF1->GetParameter(i);
gF1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.3*TMath::Abs(par);
if (we <= TMath::Abs(par)*1e-6) we = 1;
gMinuit->mnparm(i,gF1->GetParName(i),par,we,al,bl,ierf);
}
if(nfixed > 0)gMinuit->mnexcm("FIX",arglist,nfixed,ierf); // Otto
//*-*- Reset Print level
if (!Foption.Quiet) {
if (Foption.Verbose) { arglist[0] = 2; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
else { arglist[0] = 0; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
}
//*-*- Perform minimization
SetBit(kFitInit);
arglist[0] = 5000; //MaxIterations
arglist[1] = 1e-2; //epsilon
gMinuit->mnexcm("MIGRAD",arglist,2,ierf);
if (Foption.Errors) {
gMinuit->mnexcm("HESSE",arglist,0,ierf);
gMinuit->mnexcm("MINOS",arglist,0,ierf);
}
//*-*- Get return status
for (i=0;i<npar;i++) {
gMinuit->mnpout(i,gF1->GetParName(i), par,we,al,bl,ierf);
if (Foption.Errors) werr = we;
else {
gMinuit->mnerrs(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
gF1->SetParameter(i,par);
gF1->SetParError(i,werr);
}
gMinuit->mnstat(amin,edm,errdef,nvpar,nparx,icstat);
gF1->SetChisquare(amin);
//*-*- Print final values of parameters.
if (!Foption.Quiet) {
if (Foption.Errors) gMinuit->mnprin(4,amin);
else gMinuit->mnprin(3,amin);
}
delete [] arglist;
//*-*- Store fitted function in histogram functions list and draw
if (!Foption.Nostore) {
if (!Foption.Plus) fFunctions->Delete();
fnew1 = new TF1();
gF1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax);
if (TestBit(kCanDelete)) return;
if (gPad) gPad->Modified();
}
}
//______________________________________________________________________________
void TGraph::FitPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph fit options*-*-*-*-*-*
//*-* ==========================================
//
// See class TFitPanel for example
if (gPad) {
gROOT->SetSelectedPrimitive(gPad->GetSelected());
gROOT->SetSelectedPad(gPad->GetSelectedPad());
}
TList *lc = (TList*)gROOT->GetListOfCanvases();
if (!lc->FindObject("fitpanelgraph")) {
char cmd[] = "TFitPanelGraph *fitpanel = new TFitPanelGraph("fitpanelgraph","Fit Panel",300,400);";
gInterpreter->ProcessLine(cmd);
return;
}
char cmdupd[] = "fitpanelgraph->SetDefaults(); fitpanelgraph->Show();";
gInterpreter->ProcessLine(cmdupd);
}
//______________________________________________________________________________
Float_t TGraph::GetErrorX(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
Float_t TGraph::GetErrorY(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
TH1F *TGraph::GetHistogram()
{
// Returns a pointer to the histogram used to draw the axis
// Takes into account the two following cases.
// 1- option 'A' was specified in TGraph::Draw. Return fHistogram
// 2- user had called TPad::DrawFrame. return pointer to hframe histogram
if (fHistogram) return fHistogram;
if (!gPad) return 0;
gPad->Modified();
gPad->Update();
if (fHistogram) return fHistogram;
TH1F *h1 = (TH1F*)gPad->GetPrimitive("hframe");
return h1;
}
//______________________________________________________________________________
void TGraph::GetPoint(Int_t i, Float_t &x, Float_t &y)
{
//*-*-*-*-*-*-*-*-*-*-*Get x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0 || i >= fNpoints) return;
if (!fX || !fY) return;
x = fX[i];
y = fY[i];
}
//______________________________________________________________________________
TAxis *TGraph::GetXaxis()
{
// Get x axis of the graph.
if (fHistogram) return fHistogram->GetXaxis();
return 0;
}
//______________________________________________________________________________
TAxis *TGraph::GetYaxis()
{
// Get y axis of the graph.
if (fHistogram) return fHistogram->GetYaxis();
return 0;
}
//______________________________________________________________________________
void GraphFitChisquare(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag)
{
//*-*-*-*-*-*Minimization function for Graphs using a Chisquare method*-*-*-*-*
//*-* =========================================================
Double_t cu,eu,fu,fsum;
Double_t dersum[25], grad[25];
static Double_t eysum[50];
Double_t x[1];
Float_t errormax;
Int_t bin, k, npfits, nparts, part;
TGraph *gr = (TGraph*)gMinuit->GetObjectFit();
Int_t n = gr->GetN();
Float_t *gx = gr->GetX();
Float_t *gy = gr->GetY();
npar = gF1->GetNpar();
Float_t cumin = gy[0];
Float_t cumax = gy[0];
if (flag == 2) for (k=0;k<npar;k++) dersum[k] = gin[k] = 0;
nparts = n/3;
if (nparts == 0) nparts = 1;
if (nparts > 40) nparts = 40;
Float_t fxmin = gF1->GetXmin();
Float_t fxmax = gF1->GetXmax();
Float_t dfx = (fxmax - fxmin)/nparts;
if (gr->TestBit(kFitInit)) {
for (part=0;part<nparts;part++) { eysum[part] = 0;}
}
gF1->InitArgs(x,u);
npfits = 0;
f = 0;
for (bin=0;bin<n;bin++) {
x[0] = gx[bin];
if (Foption.Range) {
if (x[0] < fxmin) continue;
if (x[0] > fxmax) continue;
}
cu = gy[bin];
fu = gF1->EvalPar(x,u);
eu = gr->GetErrorY(bin);
if (Foption.W1) eu = 1;
if (eu < 0) {
part = Int_t((x[0] - fxmin)/dfx);
if (part < 0) part = 0;
if (part >= nparts) part = nparts-1;
if (gr->TestBit(kFitInit)) {
eysum[part] += (cu-fu)*(cu-fu);
if (cu < cumin) cumin = cu;
if (cu > cumax) cumax = cu;
} else {
eu = eysum[part];
}
}
if (flag == 2) {
for (k=0;k<npar;k++) dersum[k] += 1; //should be the derivative
}
npfits++;
if (flag == 2) {
for (k=0;k<npar;k++) grad[k] += dersum[k]*(fu-cu)/eu; dersum[k] = 0;
}
if (eu) fsum = (cu-fu)/eu;
else fsum = cu-fu;
f += fsum*fsum;
}
// make a better error estimate to be used in the next iterations
if (gr->TestBit(kFitInit)) {
gr->ResetBit(kFitInit);
errormax = 0.2*(cumax-cumin);
for (part=0;part<nparts;part++) {
eysum[part] = TMath::Sqrt(eysum[part]);
if (eysum[part] > errormax) eysum[part] = errormax;
if (errormax < 0.2) eysum[part] = 1;
}
}
gF1->SetNumberFitPoints(npfits);
}
//______________________________________________________________________________
void TGraph::InitGaus()
{
//*-*-*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
//*-* ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
static Double_t sqrtpi = 2.506628;
//*-*- Compute mean value and RMS of the graph in the given range
allcha = sumx = sumx2 = 0;
for (bin=0;bin<fNpoints;bin++) {
x = fX[bin];
val = fY[bin];
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
Float_t binwidx = TMath::Abs((fX[fNpoints-1] - fX[0])/fNpoints);
if (rms == 0) rms = 1;
gF1->SetParameter(0,binwidx*allcha/(sqrtpi*rms));
gF1->SetParameter(1,mean);
gF1->SetParameter(2,rms);
}
//______________________________________________________________________________
void TGraph::InitExpo()
{
//*-*-*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
//*-* =======================================================
Double_t constant, slope;
Int_t ifail;
Int_t nchanx = xlast - xfirst + 1;
LeastSquareLinearFit(-nchanx, constant, slope, ifail);
gF1->SetParameter(0,constant);
gF1->SetParameter(1,slope);
}
//______________________________________________________________________________
void TGraph::InitPolynom()
{
//*-*-*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
//*-* ===================================================
Double_t fitpar[25];
Int_t nchanx = xlast - xfirst + 1;
Int_t npar = gF1->GetNpar();
LeastSquareFit( nchanx, npar, fitpar);
for (Int_t i=0;i<npar;i++) gF1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void TGraph::LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
//*-*-*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
//*-* =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
//
static Double_t zero = 0.;
static Double_t one = 1.;
static Int_t idim = 20;
static Double_t b[400] /* was [20][20] */;
static Int_t i, k, l, ifail;
static Double_t power;
static Double_t da[20], xk, yk;
if (m <= 2) {
LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Float_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
for (k = 0; k < fNpoints; ++k) {
xk = fX[k];
yk = fY[k];
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
if (ifail < 0) {
a[0] = fY[0];
for (i=1; i<m; ++i) a[i] = 0;
return;
}
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void TGraph::LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
//*-*-*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
//*-* =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
static Double_t xbar, ybar, x2bar;
static Int_t i, n;
static Double_t xybar;
static Float_t fn, xk, yk;
static Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
for (i = 0; i < fNpoints; ++i) {
xk = fX[i];
yk = fY[i];
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Float_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void TGraph::Paint(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ===========================================
if (strstr(option,"H") || strstr(option,"h")) {
PaintGrapHist(fNpoints, fX, fY, option);
} else {
PaintGraph(fNpoints, fX, fY, option);
}
TObject *f;
if (fFunctions) {
TIter next(fFunctions);
while ((f = (TObject*) next())) {
if (f->IsA() == TF1::Class()) f->Paint("lsame");
else f->Paint();
}
}
}
//______________________________________________________________________________
void TGraph::PaintGraph(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Control function to draw a graph*-*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or X(2) : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or Y(2) : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='F' : A fill area is drawn ('CF' draw a smooth fill area)
//
// chopt='A' : Axis are drawn around the graph
//
// chopt='C' : A smooth Curve is drawn
//
// chopt='*' : A Star is plotted at each point
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart is drawn at each point
//
// chopt='1' : ylow=rwymin
//
//
Int_t OptionLine , OptionAxis , OptionCurve,OptionStar ,OptionMark;
Int_t OptionBar , OptionR , OptionOne;
Int_t OptionFill , OptionZ ,OptionCurveFill;
Int_t i, npt, nloop;
Int_t drawtype;
Float_t xlow, xhigh, ylow, yhigh;
Float_t barxmin, barxmax, barymin, barymax;
Float_t uxmin, uxmax;
Float_t x1, xn, y1, yn;
Float_t dbar, bdelta;
//*-* ______________________________________
if (npoints <= 0) {
Error("PaintGraph", "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("R")) OptionR = 1; else OptionR = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
OptionZ = 0;
//*-* If no "drawing" option is selected and if chopt<>' '
//*-* nothing is done.
if (OptionLine+OptionFill+OptionCurve+OptionStar+OptionMark+OptionBar == 0) {
if (strlen(chopt) == 0) OptionLine=1;
else return;
}
if (OptionStar) SetMarkerStyle(3);
OptionCurveFill = 0;
if (OptionCurve && OptionFill) {
OptionCurveFill = 1;
OptionFill = 0;
}
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- Draw the Axis with a fixed number of division: 510
Float_t rwxmin,rwxmax, rwymin, rwymax, maximum, minimum;
if (OptionAxis) {
rwxmin = rwxmax = x[0];
rwymin = rwymax = y[0];
for (i=1;i<npoints;i++) {
if (x[i] < rwxmin) rwxmin = x[i];
if (x[i] > rwxmax) rwxmax = x[i];
if (y[i] < rwymin) rwymin = y[i];
if (y[i] > rwymax) rwymax = y[i];
}
ComputeRange(rwxmin, rwymin, rwxmax, rwymax); //this is redefined in TGraphErrors
if (rwxmin == rwxmax) rwxmax += 1.;
if (rwymin == rwymax) rwymax += 1.;
Float_t dx = 0.1*(rwxmax-rwxmin);
Float_t dy = 0.1*(rwymax-rwymin);
uxmin = rwxmin - dx;
uxmax = rwxmax + dx;
minimum = rwymin - dy;
maximum = rwymax + dy;
if (fMinimum != -1111) rwymin = minimum = fMinimum;
if (fMaximum != -1111) rwymax = maximum = fMaximum;
if (uxmin < 0 && rwxmin >= 0) {
if (gPad->GetLogx()) uxmin = 0.9*rwxmin;
else uxmin = 0;
}
if (uxmax > 0 && rwxmax <= 0) {
if (gPad->GetLogx()) uxmax = 1.1*rwxmax;
else uxmax = 0;
}
if (minimum < 0 && rwymin >= 0) {
if(gPad->GetLogy()) minimum = 0.9*rwymin;
else minimum = 0;
}
if (maximum > 0 && rwymax <= 0) {
if(gPad->GetLogy()) maximum = 1.1*rwymax;
else maximum = 0;
}
if (minimum <= 0 && gPad->GetLogy()) minimum = 0.001*maximum;
if (uxmin <= 0 && gPad->GetLogx()) {
if (uxmax > 1000) uxmin = 1;
else uxmin = 0.001*uxmax;
}
rwxmin = uxmin;
rwxmax = uxmax;
rwymin = minimum;
rwymax = maximum;
if (fHistogram) {
fHistogram->SetMinimum(rwymin);
fHistogram->SetMaximum(rwymax);
fHistogram->GetXaxis()->SetLimits(rwxmin,rwxmax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
}
//*-*- Create a temporary histogram and fill each channel with the function value
if (!fHistogram) {
fHistogram = new TH1F((char*)GetName(),(char*)GetTitle(),40,rwxmin,rwxmax);
if (!fHistogram) return;
fHistogram->SetMinimum(rwymin);
fHistogram->SetBit(kNoStats);
fHistogram->SetMaximum(rwymax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
fHistogram->SetDirectory(0);
}
fHistogram->Paint();
}
TF1 *fit = 0;
if (fFunctions) fit = (TF1*)fFunctions->First();
if (fit) {
if (fHistogram) {
fHistogram->PaintStat(0,fit);
} else {
TH1F *hfit = new TH1F("___0","",2,0,1);
hfit->PaintStat(0,fit);
delete hfit;
}
}
rwxmin = gPad->GetUxmin();
rwxmax = gPad->GetUxmax();
rwymin = gPad->GetUymin();
rwymax = gPad->GetUymax();
uxmin = gPad->PadtoX(rwxmin);
uxmax = gPad->PadtoX(rwxmax);
if (fHistogram) {
maximum = fHistogram->GetMaximum();
minimum = fHistogram->GetMinimum();
} else {
maximum = gPad->PadtoY(rwymax);
minimum = gPad->PadtoY(rwymin);
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Draw the graph with a polyline or a fill area
if (OptionLine || OptionFill) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
nloop = npoints;
if (OptionFill && (xn != x1 || yn != y1)) nloop++;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == nloop) {
ComputeLogs(npt, OptionZ);
Int_t bord = gStyle->GetDrawBorder();
if (OptionR) {
if (OptionFill) {
gPad->PaintFillArea(npt,yworkl,xworkl);
if (bord) gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else {
if (OptionFill) {
gPad->PaintFillArea(npt,xworkl,yworkl);
if (bord) gPad->PaintPolyLine(npt,xworkl,yworkl);
}
else gPad->PaintPolyLine(npt,xworkl,yworkl);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
}
}
//*-*- Draw the graph with a smooth Curve. Smoothing via Smooth
if (OptionCurve) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
drawtype = 1;
nloop = npoints;
if (OptionCurveFill) {
drawtype += 1000;
if (xn != x1 || yn != y1) nloop++;
}
if (!OptionR) {
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (yworkl[npt-1] < rwymin || yworkl[npt-1] > rwymax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=0;i<nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype += 10;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (xworkl[npt-1] < rwxmin || xworkl[npt-1] > rwxmax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=1;i<=nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the graph with a '*' on every points
if (OptionStar) {
SetMarkerStyle(3);
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph with the current polymarker on
//*-*- every points
if (OptionMark) {
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph as a bar chart
if (OptionBar) {
if (!OptionR) {
barxmin = x[0];
barxmax = x[0];
for (i=1;i<npoints;i++) {
if (x[i] < barxmin) barxmin = x[i];
if (x[i] > barxmax) barxmax = x[i];
}
bdelta = (barxmax-barxmin)/float(npoints);
}
else {
barymin = y[0];
barymax = y[0];
for (i=1;i<npoints;i++) {
if (y[i] < barymin) barymin = y[i];
if (y[i] > barymax) barymax = y[i];
}
bdelta = (barymax-barymin)/float(npoints);
}
dbar = 0.5*bdelta*gStyle->GetBarWidth();
if (!OptionR) {
for (i=1;i<=npoints;i++) {
xlow = x[i-1] - dbar;
xhigh = x[i-1] + dbar;
yhigh = y[i-1];
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
if (yworkl[0] < gPad->GetUymin()) yworkl[0] = gPad->GetUymin();
if (yworkl[1] < gPad->GetUymin()) continue;
if (yworkl[1] > gPad->GetUymax()) yworkl[0] = gPad->GetUymax();
if (yworkl[0] > gPad->GetUymax()) continue;
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
else {
for (i=1;i<=npoints;i++) {
xhigh = x[i-1];
ylow = y[i-1] - dbar;
yhigh = y[i-1] + dbar;
xlow = TMath::Max((Float_t)0, gPad->GetUxmin());
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::PaintGrapHist(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*Control function to draw a graphistogram*-*-*-*-*-*-*-*-*-*
//*-* ========================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or x[1] : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or y[1] : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='R' : Graph is drawn horizontaly, parallel to X axis.
// (default is vertically, parallel to Y axis)
// If option R is selected the user must give:
// 2 values for Y (y[0]=YMIN and y[1]=YMAX)
// N values for X, one for each channel.
// Otherwise the user must give:
// N values for Y, one for each channel.
// 2 values for X (x[0]=XMIN and x[1]=XMAX)
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='H' : An Histogram with equidistant bins is drawn
// as a polyline.
//
// chopt='F' : An histogram with equidistant bins is drawn
// as a fill area. Contour is not drawn unless
// chopt='H' is also selected..
//
// chopt='N' : Non equidistant bins (default is equidistant)
// If N is the number of channels array X and Y
// must be dimensionned as follow:
// If option R is not selected (default) then
// the user must give:
// (N+1) values for X (limits of channels).
// N values for Y, one for each channel.
// Otherwise the user must give:
// (N+1) values for Y (limits of channels).
// N values for X, one for each channel.
//
// chopt='F1': Idem as 'F' except that fill area is no more
// reparted arround axis X=0 or Y=0 .
//
// chopt='C' : A smooth Curve is drawn.
//
// chopt='*' : A Star is plotted at the center of each bin.
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart with equidistant bins is drawn as fill
// areas (Contours are drawn).
//
//
static const char *where = "PaintGraphHist";
const Int_t NPMXFA= 99;
Int_t OptionLine , OptionAxis , OptionCurve, OptionStar , OptionMark;
Int_t OptionBar , OptionRot , OptionOne;
Int_t OptionFill , OptionZ;
Int_t OptionHist , OptionBins , OptionMarker;
Int_t i, j, npt;
Int_t drawtype, drawborder, drawbordersav;
Float_t xlow, xhigh, ylow, yhigh;
Float_t wmin, wmax;
Float_t dbar, offset, wminstep;
Float_t delta = 0;
Float_t ylast = 0;
Float_t xi, xi1, xj, xj1, yi1, yi, yj, yj1, xwmin, ywmin;
Int_t first, last, nbins;
Int_t fillarea;
static char choptaxis[10] = " ";
//*-* ______________________________________
if (npoints <= 0) {
Error(where, "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("H")) OptionHist = 1; else OptionHist = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("R")) OptionRot = 1; else OptionRot = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("N")) OptionBins = 1; else OptionBins = 0;
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- If necessary the adresses of the vectors are saved in
//*-*- a link area.
OptionZ = 1;
if (OptionStar) SetMarkerStyle(3);
first = 1;
last = npoints;
nbins = last - first + 1;
//*-*- Draw the Axis with a fixed number of division: 510
Float_t baroffset = gStyle->GetBarOffset();
Float_t barwidth = gStyle->GetBarWidth();
Float_t rwxmin = gPad->GetUxmin();
Float_t rwxmax = gPad->GetUxmax();
Float_t rwymin = gPad->GetUymin();
Float_t rwymax = gPad->GetUymax();
Float_t uxmin = gPad->PadtoX(rwxmin);
Float_t uxmax = gPad->PadtoX(rwxmax);
Float_t rounding = (uxmax-uxmin)*1.e-5;
drawborder = gStyle->GetDrawBorder();
if (OptionAxis) {
Int_t nx1, nx2, ndivx, ndivy, ndiv;
choptaxis[0] = 0;
Float_t rwmin = rwxmin;
Float_t rwmax = rwxmax;
ndivx = gStyle->GetNdivisions("X");
ndivy = gStyle->GetNdivisions("Y");
if (ndivx > 1000) {
nx2 = ndivx/100;
nx1 = TMath::Max(1, ndivx%100);
ndivx = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsWNDC());
}
ndiv =TMath::Abs(ndivx);
if (ndivx < 0) strcat(choptaxis, "N");
if (gPad->GetGridx()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogx()) {
rwmin = TMath::Power(10,rwxmin);
rwmax = TMath::Power(10,rwxmax);
strcat(choptaxis, "G");
}
TGaxis *axis = new TGaxis();
axis->SetLineColor(gStyle->GetAxisColor("X"));
axis->SetTextColor(gStyle->GetLabelColor("X"));
axis->SetTextFont(gStyle->GetLabelFont("X"));
axis->SetLabelSize(gStyle->GetLabelSize("X"));
axis->SetLabelOffset(gStyle->GetLabelOffset("X"));
axis->SetTickSize(gStyle->GetTickLength("X"));
axis->PaintAxis(rwxmin,rwymin,rwxmax,rwymin,rwmin,rwmax,ndiv,choptaxis);
choptaxis[0] = 0;
rwmin = rwymin;
rwmax = rwymax;
if (ndivy < 0) {
nx2 = ndivy/100;
nx1 = TMath::Max(1, ndivy%100);
ndivy = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsHNDC());
strcat(choptaxis, "N");
}
ndiv =TMath::Abs(ndivy);
if (gPad->GetGridy()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogy()) {
rwmin = TMath::Power(10,rwymin);
rwmax = TMath::Power(10,rwymax);
strcat(choptaxis,"G");
}
axis->SetLineColor(gStyle->GetAxisColor("Y"));
axis->SetTextColor(gStyle->GetLabelColor("Y"));
axis->SetTextFont(gStyle->GetLabelFont("Y"));
axis->SetLabelSize(gStyle->GetLabelSize("Y"));
axis->SetLabelOffset(gStyle->GetLabelOffset("Y"));
axis->SetTickSize(gStyle->GetTickLength("Y"));
axis->PaintAxis(rwxmin,rwymin,rwxmin,rwymax,rwmin,rwmax,ndiv,choptaxis);
delete axis;
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Min-Max scope
if (!OptionRot) {wmin = x[0]; wmax = x[1];}
else {wmin = y[0]; wmax = y[1];}
if (!OptionBins) delta = (wmax - wmin)/ float(nbins);
//*-*- Draw the histogram with a fill area
if (OptionFill && !OptionCurve) {
fillarea = kTRUE;
if (!OptionRot) {
xwork[0] = wmin;
if (!OptionOne) ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
else ywork[0] = gPad->GetUymin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((j-first+1)*delta);
}
else {
xj1 = x[j]; xj = x[j-1];
if (xj1 < xj) {
if (j != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j];
}
ywork[npt-1] = y[j-1];
ywork[npt] = y[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (j == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
xwork[0] = xwork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++) {
}
else {
ywork[0] = wmin;
if (!OptionOne) xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
else xwork[0] = gPad->GetUxmin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((j-first+1)*delta);
}
else {
yj1 = y[j]; yj = y[j-1];
if (yj1 < yj) {
if (j != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[j-1]; ywork[npt] = y[j];
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (j == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
ywork[0] = ywork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++)
}
}
//*-*- Draw a standard Histogram (default)
if ((OptionHist) || strlen(chopt) == 0) {
if (!OptionRot) {
xwork[0] = wmin;
// ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
ywork[0] = gPad->GetUymin();
ywmin = ywork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((i-first+1)*delta);
}
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i];
}
ywork[npt-1] = y[i-1];
ywork[npt] = y[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (i == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
else {
ywork[0] = wmin;
xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
xwmin = xwork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((i-first+1)*delta);
}
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1]; ywork[npt] = y[i];
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (i == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
}
//*-*- Draw the histogram with a smooth Curve. The computing
//*-*- of the smoothing is done by the routine IGRAP1
if (OptionCurve) {
if (!OptionFill) drawtype = 1;
else {
if (!OptionOne) drawtype = 2;
else drawtype = 3;
}
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
ComputeLogs(npt, OptionZ);
if ((yworkl[npt] < rwymin) || (yworkl[npt] > rwymax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype = drawtype+10;
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
ComputeLogs(npt, OptionZ);
if ((xworkl[npt] < uxmin) || (xworkl[npt] > uxmax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the histogram with a simple line
OptionMarker = 0;
if ((OptionStar) || (OptionMark))OptionMarker=1;
if ((OptionMarker) || (OptionLine)) {
wminstep = wmin + 0.5*delta;
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wminstep + (i-first)*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
if ((ywork[npt-1] < rwymin) || (ywork[npt-1] > rwymax)) {
if ((ywork[npt-1] < rwymin)) ywork[npt-1] = rwymin;
if ((ywork[npt-1] > rwymax)) ywork[npt-1] = rwymax;
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
else {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wminstep+(i-first)*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
if ((xwork[npt-1] < uxmin) || (xwork[npt-1] > uxmax)) {
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine != 0 && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
}
//*-*- Draw the histogram as a bar chart
if (OptionBar) {
if (!OptionBins) { offset = delta*baroffset; dbar = delta*barwidth; }
else {
if (!OptionRot) {
offset = (x[1]-x[0])*baroffset;
dbar = (x[1]-x[0])*barwidth;
} else {
offset = (y[1]-y[0])*baroffset;
dbar = (y[1]-y[0])*barwidth;
}
}
drawbordersav = drawborder;
gStyle->SetDrawBorder(1);
if (!OptionRot) {
xlow = wmin+offset;
xhigh = wmin+offset+dbar;
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
for (i=first; i<=last;i++) {
yhigh = y[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
if (!OptionBins) {
xlow = xlow+delta;
xhigh = xhigh+delta;
}
else {
if (i < last) {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
Error(where, "X must be in increasing order");
return;
}
offset = (x[i+1]-x[i])*baroffset;
dbar = (x[i+1]-x[i])*barwidth;
xlow = x[i] + offset;
xhigh = x[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
else {
ylow = wmin + offset;
yhigh = wmin + offset + dbar;
if (!OptionOne) xlow = TMath::Max((Float_t)0,gPad->GetUxmin());
else xlow = gPad->GetUxmin();
for (i=first; i<=last;i++) {
xhigh = x[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
gPad->PaintBox(xlow,ylow,xhigh,yhigh);
if (!OptionBins) {
ylow = ylow + delta;
yhigh = yhigh + delta;
}
else {
if (i < last) {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
Error(where, "Y must be in increasing order");
return;
}
offset = (y[i+1]-y[i])*baroffset;
dbar = (y[i+1]-y[i])*barwidth;
ylow = y[i] + offset;
yhigh = y[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
gStyle->SetDrawBorder(drawbordersav);
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::ComputeLogs(Int_t npoints, Int_t opt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Convert WC from Log scales*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==========================
//
// Take the LOG10 of xwork and ywork according to the value of Options
// and put it in xworkl and yworkl.
//
// npoints : Number of points in xwork and in ywork.
//
for (Int_t i=0;i<npoints;i++) {
xworkl[i] = xwork[i];
yworkl[i] = ywork[i];
if (gPad->GetLogx()) {
if (xworkl[i] > 0) xworkl[i] = TMath::Log10(xworkl[i]);
else xworkl[i] = gPad->GetX1();
}
if (!opt && gPad->GetLogy()) {
if (yworkl[i] > 0) yworkl[i] = TMath::Log10(yworkl[i]);
else yworkl[i] = gPad->GetY1();
}
// if (yworkl[i] > gPad->GetUymax()) yworkl[i] = gPad->GetUymax();
}
}
//______________________________________________________________________________
void TGraph::Print(Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Print graph values*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==================
for (Int_t i=0;i<fNpoints;i++) {
printf("x[%d]=%g, y[%d]=%gn",i,fX[i],i,fY[i]);
}
}
//______________________________________________________________________________
void TGraph::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
char quote = '"';
out<<" "<<endl;
if (gROOT->ClassSaved(TGraph::Class())) {
out<<" ";
} else {
out<<" TGraph *";
}
out<<"graph = new TGraph("<<fNpoints<<");"<<endl;
out<<" graph->SetName("<<quote<<GetName()<<quote<<");"<<endl;
out<<" graph->SetTitle("<<quote<<GetTitle()<<quote<<");"<<endl;
SaveFillAttributes(out,"graph",0,1001);
SaveLineAttributes(out,"graph",1,1,1);
SaveMarkerAttributes(out,"graph",1,1,1);
for (Int_t i=0;i<fNpoints;i++) {
out<<" graph->SetPoint("<<i<<","<<fX[i]<<","<<fY[i]<<");"<<endl;
}
out<<" graph->Draw("
<<quote<<option<<quote<<");"<<endl;
}
//______________________________________________________________________________
void TGraph::SetMaximum(Float_t maximum)
{
fMaximum = maximum;
if (fHistogram) fHistogram->SetMaximum(maximum);
}
//______________________________________________________________________________
void TGraph::SetMinimum(Float_t minimum)
{
fMinimum = minimum;
if (fHistogram) fHistogram->SetMinimum(minimum);
}
//______________________________________________________________________________
void TGraph::SetPoint(Int_t i, Float_t x, Float_t y)
{
//*-*-*-*-*-*-*-*-*-*-*Set x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0) return;
if (i >= fNpoints) {
// re-allocate the object
Float_t *savex = new Float_t[i+1];
Float_t *savey = new Float_t[i+1];
if (fNpoints > 0) {
memcpy(savex,fX,fNpoints*sizeof(Float_t));
memcpy(savey,fY,fNpoints*sizeof(Float_t));
}
if (fX) delete [] fX;
if (fY) delete [] fY;
fX = savex;
fY = savey;
fNpoints = i+1;
}
fX[i] = x;
fY[i] = y;
}
//______________________________________________________________________________
void TGraph::Smooth(Int_t npoints, Float_t *x, Float_t *y, Int_t drawtype)
{
//*-*-*-*-*-*-*-*-*-*-*-*Smooth a curve given by N points*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
// Underlaying routine for Draw based on the CERN GD3 routine TVIPTE
//
// Author - Marlow etc. Modified by - P. Ward Date - 3.10.1973
//
// This routine draws a smooth tangentially continuous curve through
// the sequence of data points P(I) I=1,N where P(I)=(X(I),Y(I))
// the curve is approximated by a polygonal arc of short vectors .
// the data points can represent open curves, P(1) != P(N) or closed
// curves P(2) == P(N) . If a tangential discontinuity at P(I) is
// required , then set P(I)=P(I+1) . loops are also allowed .
//
// Reference Marlow and Powell,Harwell report No.R.7092.1972
// MCCONALOGUE,Computer Journal VOL.13,NO4,NOV1970PP392 6
//
// _Input parameters:
//
// npoints : Number of data points.
// x : Abscissa
// y : Ordinate
//
//
// delta is the accuracy required in constructing the curve.
// if it is zero then the routine calculates a value other-
// wise it uses this value. (default is 0.0)
//
//
Int_t i, k, kp, km, NpointsMax, banksize, n2, npt;
Int_t maxiterations, finished;
Int_t jtype, ktype, closed;
Float_t sxmin, sxmax, symin, symax;
Float_t delta;
Float_t xorg, yorg;
Float_t ratio_signs, xratio, yratio;
Int_t flgic, flgis;
Int_t iw, loptx;
Float_t P1, P2, P3, P4, P5, P6;
Float_t W1, W2, W3;
Float_t A, B, C, R, S, T, Z;
Float_t CO, SO, CT, ST, CTU, STU, XNT;
Float_t DX1, DY1, DX2, DY2, DK1, DK2;
Float_t XO, YO, DX, DY, XT, YT;
Float_t XA, XB, YA, YB;
Float_t U1, U2, U3, TJ;
Float_t CC, ERR;
Float_t SB, STH;
Float_t wsign, tsquare, tcube;
C = T = CO = SO = CT = ST = CTU = STU = DX1 = DY1 = DX2 = DY2 = 0;
XT = YT = XA = XB = YA = YB = U1 = U2 = U3 = TJ = SB = 0;
//*-* ______________________________________
NpointsMax = npoints*10;
n2 = NpointsMax-2;
banksize = n2;
Float_t *qlx = new Float_t[NpointsMax];
Float_t *qly = new Float_t[NpointsMax];
if (!qlx || !qly) {
Error("Smooth", "not enough space in memory");
return;
}
//*-*- Decode the type of curve according to
//*-*- chopt of IGHIST.
//*-*- ('S', 'SA', 'SA1' ,'XS', 'XSA', or 'XSA1')
if (drawtype >= 1000) drawtype -= 1000;
loptx = kFALSE;
jtype = drawtype-10;
if (jtype > 0) { ktype = jtype; loptx = kTRUE; }
else ktype = drawtype;
Float_t ruxmin = gPad->GetUxmin();
Float_t ruymin = gPad->GetUymin();
if (ktype == 3) {
xorg = ruxmin;
yorg = ruymin;
} else {
xorg = TMath::Max((Float_t)0,ruxmin);
yorg = TMath::Max((Float_t)0,ruymin);
}
maxiterations = 20;
delta = 0.00055;
//*-*- Scale data to the range 0-ratio_signs in X, 0-1 in Y
//*-*- where ratio_signs is the ratio between the number of changes
//*-*- of sign in Y divided by the number of changes of sign in X
sxmin = x[0];
sxmax = x[0];
symin = y[0];
symax = y[0];
Float_t six = 1;
Float_t siy = 1;
for (i=1;i<npoints;i++) {
if (i > 1) {
if ((x[i]-x[i-1])*(x[i-1]-x[i-2]) < 0) six++;
if ((y[i]-y[i-1])*(y[i-1]-y[i-2]) < 0) siy++;
}
if (x[i] < sxmin) sxmin = x[i];
if (x[i] > sxmax) sxmax = x[i];
if (y[i] < symin) symin = y[i];
if (y[i] > symax) symax = y[i];
}
closed = 0;
Float_t dx1n = TMath::Abs(x[npoints-1]-x[0]);
Float_t dy1n = TMath::Abs(y[npoints-1]-y[0]);
if (dx1n < 0.01*(sxmax-sxmin) && dy1n < 0.01*(symax-symin)) closed = 1;
if (sxmin == sxmax) xratio = 1;
else {
if (six > 1) ratio_signs = siy/six;
else ratio_signs = 20;
xratio = ratio_signs/(sxmax-sxmin);
}
if (symin == symax) yratio = 1;
else yratio = 1/(symax-symin);
qlx[0] = x[0];
qly[0] = y[0];
for (i=0;i<npoints;i++) {
x[i] = (x[i]-sxmin)*xratio;
y[i] = (y[i]-symin)*yratio;
}
//*-*- finished is minus one if we must draw a straight line from P(k-1)
//*-*- to P(k). finished is one if the last call to IPL has < N2
//*-*- points. finished is zero otherwise. npt counts the X and Y
//*-*- coordinates in work . When npt=N2 a call to IPL is made.
finished = 0;
npt = 1;
k = 1;
//*-*- Convert coordinates back to original system
//*-*- Separate the set of data points into arcs P(k-1),P(k).
//*-*- Calculate the direction cosines. first consider whether
//*-*- there is a continuous tangent at the endpoints.
if (!closed) {
if (x[0] != x[npoints-1] || y[0] != y[npoints-1]) goto L40;
if (x[npoints-2] == x[npoints-1] && y[npoints-2] == y[npoints-1]) goto L40;
if (x[0] == x[1] && y[0] == y[1]) goto L40;
}
flgic = kFALSE;
flgis = kTRUE;
//*-*- flgic is true if the curve is open and false if it is closed.
//*-*- flgis is true in the main loop, but is false if there is
//*-*- a deviation from the main loop.
km = npoints - 1;
//*-*- Calculate direction cosines at P(1) using P(N-1),P(1),P(2).
goto L100;
L40:
flgic = kTRUE;
flgis = kFALSE;
//*-*- Skip excessive consecutive equal points.
L50:
if (k >= npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
k++;
if (x[k-1] == x[k-2] && y[k-1] == y[k-2]) goto L50;
L60:
km = k-1;
if (k > npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
if (k < npoints) goto L90;
if (!flgic) { kp = 2; goto L130;}
L80:
if (flgis) goto L150;
//*-*- Draw a straight line from P(k-1) to P(k).
finished = -1;
goto L170;
//*-*- Test whether P(k) is a cusp.
L90:
if (x[k-1] == x[k] && y[k-1] == y[k]) goto L80;
L100:
kp = k+1;
goto L130;
//*-*- Branch if the next section of the curve begins at a cusp.
L110:
if (!flgis) goto L50;
//*-*- Carry forward the direction cosines from the previous arc.
L120:
CO = CT;
SO = ST;
k++;
goto L60;
//*-*- Calculate the direction cosines at P(k). If k=1 then
//*-*- N-1 is used for k-1. If k=N then 2 is used for k+1.
//*-*- direction cosines at P(k) obtained from P(k-1),P(k),P(k+1).
L130:
DX1 = x[k-1] - x[km-1];
DY1 = y[k-1] - y[km-1];
DK1 = DX1*DX1 + DY1*DY1;
DX2 = x[kp-1] - x[k-1];
DY2 = y[kp-1] - y[k-1];
DK2 = DX2*DX2 + DY2*DY2;
CTU = DX1*DK2 + DX2*DK1;
STU = DY1*DK2 + DY2*DK1;
XNT = CTU*CTU + STU*STU;
//*-*- If both ctu and stu are zero,then default.This can
//*-*- occur when P(k)=P(k+1). I.E. A loop.
if (XNT < 1.E-25) {
CTU = DY1;
STU =-DX1;
XNT = DK1;
}
//*-*- Normalise direction cosines.
CT = CTU/TMath::Sqrt(XNT);
ST = STU/TMath::Sqrt(XNT);
if (flgis) goto L160;
//*-*- Direction cosines at P(k-1) obtained from P(k-1),P(k),P(k+1).
W3 = 2*(DX1*DY2-DX2*DY1);
CO = CTU+W3*DY1;
SO = STU-W3*DX1;
XNT = 1/TMath::Sqrt(CO*CO+SO*SO);
CO = CO*XNT;
SO = SO*XNT;
flgis = kTRUE;
goto L170;
//*-*- Direction cosines at P(k) obtained from P(k-2),P(k-1),P(k).
L150:
W3 = 2*(DX1*DY2-DX2*DY1);
CT = CTU-W3*DY2;
ST = STU+W3*DX2;
XNT = 1/TMath::Sqrt(CT*CT+ST*ST);
CT = CT*XNT;
ST = ST*XNT;
flgis = kFALSE;
goto L170;
L160:
if (k <= 1) goto L120;
//*-*- For the arc between P(k-1) and P(k) with direction cosines CO,
//*-*- SO and CT,ST respectively, calculate the coefficients of the
//*-*- parametric cubic represented by X(T) and Y(T) where
//*-*- X(T)=XA*T**3 + XB*T**2 + CO*T + XO
//*-*- Y(T)=YA*T**3 + YB*T**2 + SO*T + YO
L170:
XO = x[k-2];
YO = y[k-2];
DX = x[k-1] - XO;
DY = y[k-1] - YO;
//*-*- Initialise the values of X(TI),Y(TI) in XT and YT respectively.
XT = XO;
YT = YO;
if (finished < 0) { //*-*- Draw a straight line between (XO,YO) and (XT,YT)
XT += DX;
YT += DY;
goto L300;
}
C = DX*DX+DY*DY;
A = CO+CT;
B = SO+ST;
R = DX*A+DY*B;
T = C*6/(TMath::Sqrt(R*R+2*(7-CO*CT-SO*ST)*C)+R);
tsquare = T*T;
tcube = T*tsquare;
XA = (A*T-2*DX)/tcube;
XB = (3*DX-(CO+A)*T)/tsquare;
YA = (B*T-2*DY)/tcube;
YB = (3*DY-(SO+B)*T)/tsquare;
//*-*- If the curve is close to a straight line then use a straight
//*-*- line between (XO,YO) and (XT,YT).
if (.75*TMath::Max(TMath::Abs(DX*SO-DY*CO),TMath::Abs(DX*ST-DY*CT)) <= delta) {
finished = -1;
XT += DX;
YT += DY;
goto L300;
}
//*-*- Calculate a set of values 0 == T(0).LTCT(1) < ... < T(M)=TC
//*-*- such that polygonal arc joining X(T(J)),Y(T(J)) (J=0,1,..M)
//*-*- is within the required accuracy of the curve
TJ = 0;
U1 = YA*XB-YB*XA;
U2 = YB*CO-XB*SO;
U3 = SO*XA-YA*CO;
//*-*- Given T(J), calculate T(J+1). The values of X(T(J)),
//*-*- Y(T(J)) T(J) are contained in XT,YT and TJ respectively.
L180:
S = T - TJ;
iw = -2;
//*-*- Define iw here later.
P1 = (2*U1)*TJ-U3;
P2 = (U1*TJ-U3)*3*TJ+U2;
P3 = 3*TJ*YA+YB;
P4 = (P3+YB)*TJ+SO;
P5 = 3*TJ*XA+XB;
P6 = (P5+XB)*TJ+CO;
//*-*- Test D(TJ,THETA). A is set to (Y(TJ+S)-Y(TJ))/S.B is
//*-*- set to (X(TJ+S)-X(TJ))/S.
CC = 0.8209285;
ERR = 0.1209835;
L190:
iw -= 2;
L200:
A = (S*YA+P3)*S+P4;
B = (S*XA+P5)*S+P6;
//*-*- Set Z to PSI(D/delta)-CC.
W1 = -S*(S*U1+P1);
W2 = S*S*U1-P2;
W3 = 1.5*W1+W2;
//*-*- Set the estimate of (THETA-TJ)/S.Then set the numerator
//*-*- of the expression (EQUATION 4.4)/S. Then set the square
//*-*- of D(TJ,TJ+S)/delta. Then replace Z by PSI(D/delta)-CC.
if (W3 > 0) wsign = TMath::Abs(W1);
else wsign = -TMath::Abs(W1);
STH = 0.5+wsign/(3.4*TMath::Abs(W1)+5.2*TMath::Abs(W3));
Z = S*STH*(S-S*STH)*(W1*STH+W1+W2);
Z = Z*Z/((A*A+B*B)*(delta*delta));
Z = (Z+2.642937)*Z/((.3715652*Z+3.063444)*Z+.2441889)-CC;
//*-*- Branch if Z has been calculated
if (iw > 0) goto L250;
if (Z > ERR) goto L240;
goto L220;
L210:
iw -= 2;
L220:
if (iw+2 == 0) goto L190;
if (iw+2 > 0) goto L290;
//*-*- Last part of arc.
L230:
XT = x[k-1];
YT = y[k-1];
S = 0;
goto L300;
//*-*- Z(S). find a value of S where 0 <= S <= SB such that
//*-*- TMath::Abs(Z(S)) < ERR
L240:
kp = 0;
C = Z;
SB = S;
L250:
Zero(kp,0,SB,ERR,S,Z,maxiterations);
if (kp == 2) goto L210;
if (kp > 2) {
Error("Smooth", "Attempt to plot outside plot limits");
goto L230;
}
if (iw > 0) goto L200;
//*-*- Set Z=Z(S) for S=0.
if (iw < 0) {
Z = -CC;
iw = 0;
goto L250;
}
//*-*- Set Z=Z(S) for S=SB.
Z = C;
iw = 1;
goto L250;
//*-*- Update TJ,XT and YT.
L290:
XT = XT + S*B;
YT = YT + S*A;
TJ = S + TJ;
//*-*- Convert coordinates to original system
L300:
qlx[npt] = sxmin + XT/xratio;
qly[npt] = symin + YT/yratio;
npt++;
//*-*- If a fill area must be drawn and if the banks LX and
//*-*- LY are too small they are enlarged in order to draw
//*-*- the filled area in one go.
if (npt < banksize) goto L320;
if (drawtype >= 1000 || ktype > 1) {
Int_t newsize = banksize + n2;
Float_t *qtemp = new Float_t[banksize];
for (i=0;i<banksize;i++) qtemp[i] = qlx[i];
delete [] qlx;
qlx = new Float_t[newsize];
for (i=0;i<banksize;i++) qlx[i] = qtemp[i];
for (i=0;i<banksize;i++) qtemp[i] = qly[i];
delete [] qly;
qly = new Float_t[newsize];
for (i=0;i<banksize;i++) qly[i] = qtemp[i];
delete [] qtemp;
banksize = newsize;
goto L320;
}
//*-*- Draw the graph
L310:
if (drawtype >= 1000) {
gPad->PaintFillArea(npt,qlx,qly, "B");
}
else {
if (ktype > 1) {
if (!loptx) {
qlx[npt] = qlx[npt-1];
qlx[npt+1] = qlx[0];
qly[npt] = yorg;
qly[npt+1] = yorg;
}
else {
qlx[npt] = xorg;
qlx[npt+1] = xorg;
qly[npt] = qly[npt-1];
qly[npt+1] = qly[0];
}
gPad->PaintFillArea(npt+2,qlx,qly);
}
gPad->PaintPolyLine(npt,qlx,qly);
}
npt = 1;
qlx[0] = sxmin + XT/xratio;
qly[0] = symin + YT/yratio;
L320:
if (finished > 0) goto L390;
if (finished < 0) { finished = 0; goto L110;}
if (S > 0) goto L180;
goto L110;
//*-*- Convert coordinates back to original system
L390:
for (i=0;i<npoints;i++) {
x[i] = sxmin + x[i]/xratio;
y[i] = symin + y[i]/yratio;
}
delete [] qlx;
delete [] qly;
}
//______________________________________________________________________________
void TGraph::Streamer(TBuffer &b)
{
// Stream an object of class TGraph.
if (b.IsReading()) {
b.ReadVersion(); //Version_t v = b.ReadVersion();
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNpoints;
fX = new Float_t[fNpoints];
fY = new Float_t[fNpoints];
b.ReadFastArray(fX,fNpoints);
b.ReadFastArray(fY,fNpoints);
b >> fFunctions;
b >> fHistogram;
if (fHistogram) fHistogram->SetDirectory(0);
b >> fMinimum;
b >> fMaximum;
} else {
b.WriteVersion(TGraph::IsA());
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b << fNpoints;
b.WriteFastArray(fX,fNpoints);
b.WriteFastArray(fY,fNpoints);
b << fFunctions;
b << (TObject *)fHistogram;
b << fMinimum;
b << fMaximum;
}
}
//______________________________________________________________________________
void TGraph::Zero(Int_t &k,Float_t AZ,Float_t BZ,Float_t E2,Float_t &X,Float_t &Y
,Int_t maxiterations)
{
//*-*-*-*-*-*-*-*-*-*-*-*Find zero of a continuous function*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// Underlaying routine for PaintGraph
// This function finds a real zero of the continuous real
// function Y(X) in a given interval (A,B). See accompanying
// notes for details of the argument list and calling sequence
//
//
static Float_t A, B, YA, ytest, Y1, X1, H;
static Int_t J1, IT, J3, J2;
Float_t YB, X2;
YB = 0;
//*-*______________________________________
//*-*- Calculate Y(X) at X=AZ.
if (k <= 0) {
A = AZ;
B = BZ;
X = A;
J1 = 1;
IT = 1;
k = J1;
return;
}
//*-*- Test whether Y(X) is sufficiently small.
if (TMath::Abs(Y) <= E2) { k = 2; return; }
//*-*- Calculate Y(X) at X=BZ.
if (J1 == 1) {
YA = Y;
X = B;
J1 = 2;
return;
}
//*-*- Test whether the signs of Y(AZ) and Y(BZ) are different.
//*-*- if not, begin the binary subdivision.
if (J1 != 2) goto L100;
if (YA*Y < 0) goto L120;
X1 = A;
Y1 = YA;
J1 = 3;
H = B - A;
J2 = 1;
X2 = A + 0.5*H;
J3 = 1;
IT++; //*-*- Check whether (maxiterations) function values have been calculated.
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Test whether a bracket has been found .
//*-*- If not,continue the search
L100:
if (J1 > 3) goto L170;
if (YA*Y >= 0) {
if (J3 >= J2) {
H = 0.5*H; J2 = 2*J2;
A = X1; YA = Y1; X2 = A + 0.5*H; J3 = 1;
}
else {
A = X; YA = Y; X2 = X + H; J3++;
}
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- The first bracket has been found.calculate the next X by the
//*-*- secant method based on the bracket.
L120:
B = X;
YB = Y;
J1 = 4;
L130:
if (TMath::Abs(YA) > TMath::Abs(YB)) { X1 = A; Y1 = YA; X = B; Y = YB; }
else { X1 = B; Y1 = YB; X = A; Y = YA; }
//*-*- Use the secant method based on the function values Y1 and Y.
//*-*- check that X2 is inside the interval (A,B).
L150:
X2 = X-Y*(X-X1)/(Y-Y1);
X1 = X;
Y1 = Y;
ytest = 0.5*TMath::Min(TMath::Abs(YA),TMath::Abs(YB));
if ((X2-A)*(X2-B) < 0) {
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- Calculate the next value of X by bisection . Check whether
//*-*- the maximum accuracy has been achieved.
L160:
X2 = 0.5*(A+B);
ytest = 0;
if ((X2-A)*(X2-B) >= 0) { k = 2; return; }
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Revise the bracket (A,B).
L170:
if (J1 != 4) return;
if (YA*Y < 0) { B = X; YB = Y; }
else { A = X; YA = Y; }
//*-*- Use ytest to decide the method for the next value of X.
if (ytest <= 0) goto L130;
if (TMath::Abs(Y)-ytest <= 0) goto L150;
goto L160;
}
*/
//
//
//______________________________________________________________________________
TGraph::TGraph(): TNamed(), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =========================
fNpoints = 0;
fX = 0;
fY = 0;
fFunctions = 0;
fHistogram = 0;
fMaximum = -1111;
fMinimum = -1111;
}
//______________________________________________________________________________
TGraph::TGraph(Int_t n, Float_t *x, Float_t *y)
: TNamed("Graph","Graph"), TAttLine(), TAttFill(), TAttMarker()
{
//*-*-*-*-*-*-*-*-*-*-*Graph normal constructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* ========================
if (n <= 0) {
Error("TGraph", "illegal number of points (%d)", n);
return;
}
fFunctions = new TList(this);
fHistogram = 0;
fNpoints = n;
fX = new Float_t[n];
fY = new Float_t[n];
fMaximum = -1111;
fMinimum = -1111;
if (!x || !y) return;
for (Int_t i=0;i<n;i++) {
fX[i] = x[i];
fY[i] = y[i];
}
SetBit(kClipFrame);
}
//______________________________________________________________________________
TGraph::~TGraph()
{
//*-*-*-*-*-*-*-*-*-*-*Graph default destructor-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
//*-* =======================
delete [] fX;
delete [] fY;
if (!fFunctions) return;
fFunctions->Delete();
delete fFunctions;
fFunctions = 0;
delete fHistogram;
fHistogram = 0;
}
//______________________________________________________________________________
void TGraph::ComputeRange(Float_t &, Float_t &, Float_t &, Float_t &)
{
// this function is dummy in TGraph, but redefined by TGraphErrors
}
//______________________________________________________________________________
void TGraph::Draw(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ==========================================
//
// Options to draw a graph are described in TGraph::PaintGraph
char chopt[8] = " ";
if (strlen(option) < 7) strcpy(chopt,option);
else strncpy(chopt,option,7);
// in case of option *, set marker style to 3 (star) and replace
// * option by option P.
char *cstar = strchr(chopt,'*');
if (cstar) {
SetMarkerStyle(3);
cstar[0] = 'P';
}
AppendPad(chopt);
}
//______________________________________________________________________________
Int_t TGraph::DistancetoPrimitive(Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a graph*-*-*-*-*-*
//*-* ===========================================
// Compute the closest distance of approach from point px,py to this line.
// The distance is computed in pixels units.
//
//*-*- Are we on the axis?
Int_t distance;
if (fHistogram) {
distance = fHistogram->DistancetoPrimitive(px,py);
if (distance <= 0) return distance;
}
//*-*- Somewhere on the graph points?
const Int_t big = 9999;
const Int_t kMaxDiff = 10;
Int_t puxmin = gPad->XtoAbsPixel(gPad->GetUxmin());
Int_t puymin = gPad->YtoAbsPixel(gPad->GetUymin());
Int_t puxmax = gPad->XtoAbsPixel(gPad->GetUxmax());
Int_t puymax = gPad->YtoAbsPixel(gPad->GetUymax());
//*-*- return if point is not in the histogram area
if (px <= puxmin) return big;
if (py >= puymin) return big;
if (px >= puxmax) return big;
if (py <= puymax) return big;
//*-*- check if point is near one of the graph points
Int_t i, pxp, pyp, d;
distance = big;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < distance) distance = d;
}
if (distance < kMaxDiff) return distance;
for (i=0;i<fNpoints-1;i++) {
d = DistancetoLine(px, py, gPad->XtoPad(fX[i]), gPad->YtoPad(fY[i]), gPad->XtoPad(fX[i+1]), gPad->YtoPad(fY[i+1]));
if (d < distance) distance = d;
}
//*-*- Loop on the list of associated functions and user objects
TObject *f;
TIter next(fFunctions);
while ((f = (TObject*) next())) {
Int_t dist = f->DistancetoPrimitive(px,py);
if (dist < kMaxDiff) {gPad->SetSelected(f); return dist;}
}
return distance;
}
//______________________________________________________________________________
void TGraph::DrawGraph(Int_t n, Float_t *x, Float_t *y, Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with new attributes*-*-*-*-*-*-*-*-*-*
//*-* ===================================
TGraph *newgraph = new TGraph(n, x, y);
TAttLine::Copy(*newgraph);
TAttFill::Copy(*newgraph);
TAttMarker::Copy(*newgraph);
newgraph->SetBit(kCanDelete);
newgraph->AppendPad(option);
}
//______________________________________________________________________________
void TGraph::DrawPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph drawing options*-*-*-*-*-*
//*-* ==============================================
//
printf("TGraph::DrawPanel: not yet implementedn");
}
//______________________________________________________________________________
void TGraph::ExecuteEvent(Int_t event, Int_t px, Int_t py)
{
//*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
//*-* =========================================
// This member function is called when a graph is clicked with the locator
//
// If Left button clicked on one of the line end points, this point
// follows the cursor until button is released.
//
// if Middle button clicked, the line is moved parallel to itself
// until the button is released.
//
Int_t i, d;
Float_t xmin, xmax, ymin, ymax, dx, dy, dxr, dyr;
const Int_t kMaxDiff = 10;
static Bool_t MIDDLE;
static Int_t ipoint, pxp, pyp;
static Int_t px1,px2,py1,py2;
static Int_t pxold, pyold, px1old, py1old, px2old, py2old;
static Int_t dpx, dpy;
static Int_t *x=0, *y=0;
switch (event) {
case kButton1Down:
gGXW->SetLineColor(-1);
TAttLine::Modify(); //Change line attributes only if necessary
px1 = gPad->XtoAbsPixel(gPad->GetX1());
py1 = gPad->YtoAbsPixel(gPad->GetY1());
px2 = gPad->XtoAbsPixel(gPad->GetX2());
py2 = gPad->YtoAbsPixel(gPad->GetY2());
ipoint = -1;
if (x || y) break;
x = new Int_t[fNpoints+1];
y = new Int_t[fNpoints+1];
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
x[i] = pxp;
y[i] = pyp;
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) ipoint =i;
}
dpx = 0;
dpy = 0;
pxold = px;
pyold = py;
if (ipoint < 0) return;
if (ipoint == 0) {
px1old = 0;
py1old = 0;
px2old = gPad->XtoAbsPixel(fX[1]);
py2old = gPad->YtoAbsPixel(fY[1]);
} else if (ipoint == fNpoints-1) {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[fNpoints-2]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[fNpoints-2]));
px2old = 0;
py2old = 0;
} else {
px1old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint-1]));
py1old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint-1]));
px2old = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint+1]));
py2old = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint+1]));
}
pxold = gPad->XtoAbsPixel(gPad->XtoPad(fX[ipoint]));
pyold = gPad->YtoAbsPixel(gPad->YtoPad(fY[ipoint]));
break;
case kMouseMotion:
MIDDLE = kTRUE;
for (i=0;i<fNpoints;i++) {
pxp = gPad->XtoAbsPixel(gPad->XtoPad(fX[i]));
pyp = gPad->YtoAbsPixel(gPad->YtoPad(fY[i]));
d = TMath::Abs(pxp-px) + TMath::Abs(pyp-py);
if (d < kMaxDiff) MIDDLE = kFALSE;
}
//*-*- check if point is close to an axis
if (MIDDLE) gPad->SetCursor(kMove);
else gPad->SetCursor(kHand);
break;
case kButton1Motion:
if (MIDDLE) {
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
dpx += px - pxold;
dpy += py - pyold;
pxold = px;
pyold = py;
for(i=0;i<fNpoints-1;i++) {
gGXW->DrawLine(x[i]+dpx, y[i]+dpy, x[i+1]+dpx, y[i+1]+dpy);
pxp = x[i]+dpx;
pyp = y[i]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
}
pxp = x[fNpoints-1]+dpx;
pyp = y[fNpoints-1]+dpy;
gGXW->DrawLine(pxp-4, pyp-4, pxp+4, pyp-4);
gGXW->DrawLine(pxp+4, pyp-4, pxp+4, pyp+4);
gGXW->DrawLine(pxp+4, pyp+4, pxp-4, pyp+4);
gGXW->DrawLine(pxp-4, pyp+4, pxp-4, pyp-4);
} else {
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
pxold = px;
pxold = TMath::Max(pxold, px1);
pxold = TMath::Min(pxold, px2);
pyold = py;
pyold = TMath::Max(pyold, py2);
pyold = TMath::Min(pyold, py1);
if (px1old) gGXW->DrawLine(px1old, py1old, pxold, pyold);
if (px2old) gGXW->DrawLine(pxold, pyold, px2old, py2old);
gGXW->DrawLine(pxold-4, pyold-4, pxold+4, pyold-4);
gGXW->DrawLine(pxold+4, pyold-4, pxold+4, pyold+4);
gGXW->DrawLine(pxold+4, pyold+4, pxold-4, pyold+4);
gGXW->DrawLine(pxold-4, pyold+4, pxold-4, pyold-4);
}
break;
case kButton1Up:
//*-*- Compute x,y range
xmin = gPad->GetUxmin();
xmax = gPad->GetUxmax();
ymin = gPad->GetUymin();
ymax = gPad->GetUymax();
dx = xmax-xmin;
dy = ymax-ymin;
dxr = dx/(1 - gPad->GetLeftMargin() - gPad->GetRightMargin());
dyr = dy/(1 - gPad->GetBottomMargin() - gPad->GetTopMargin());
// Range() could change the size of the pad pixmap and therefore should
// be called before the other paint routines
gPad->Range(xmin - dxr*gPad->GetLeftMargin(),
ymin - dyr*gPad->GetBottomMargin(),
xmax + dxr*gPad->GetRightMargin(),
ymax + dyr*gPad->GetTopMargin());
gPad->RangeAxis(xmin, ymin, xmax, ymax);
if (MIDDLE) {
for(i=0;i<fNpoints;i++) {
fX[i] = gPad->PadtoX(gPad->AbsPixeltoX(x[i]+dpx));
fY[i] = gPad->PadtoY(gPad->AbsPixeltoY(y[i]+dpy));
}
} else {
fX[ipoint] = gPad->PadtoX(gPad->AbsPixeltoX(pxold));
fY[ipoint] = gPad->PadtoY(gPad->AbsPixeltoY(pyold));
}
delete [] x; x = 0;
delete [] y; y = 0;
gPad->Modified(kTRUE);
gGXW->SetLineColor(-1);
}
}
//______________________________________________________________________________
void TGraph::Fit(Text_t *fname, Option_t *option, Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Fit this graph with function fname*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// fname is the name of an already predefined function created by TF1
// Predefined functions such as Gaus, Expo and Poln are automatically
// created by ROOT.
//
// The list of fit options is given in parameter option.
// option = "W" Set all errors to 1
// = "Q" Quiet mode (minimum printing)
// = "V" Verbose mode (default is between Q and V)
// = "R" Use the Range specified in the function range
// = "N" Do not store the graphics function, do not draw
// = "0" Do not plot the result of the fit. By default the fitted function
// is drawn unless the option"N" above is specified.
// = "+" Add this new fitted function to the list of fitted functions
// (by default, any previous function is deleted)
//
// When the fit is drawn (by default), the parameter goption may be used
// to specify a list of graphics options. See TGraph::Paint for a complete
// list of these options.
//
// In order to use the Range option, one must first create a function
// with the expression to be fitted. For example, if your graph
// has a defined range between -4 and 4 and you want to fit a gaussian
// only in the interval 1 to 3, you can do:
// TF1 *f1 = new TF1("f1","gaus",1,3);
// graph->Fit("f1","R");
//
// You can specify boundary limits for some or all parameters via
// f1->SetParLimits(p_number, parmin, parmax);
// if parmin>=parmax, the parameter is fixed
// Note that you are not forced to fix the limits for all parameters.
// For example, if you fit a function with 6 parameters, you can do:
// func->SetParameters(0,3.1,1.e-6,0.1,-8,100);
// func->SetParLimits(4,-10,-4);
// func->SetParLimits(5, 1,1);
// With this setup, parameters 0->3 can vary freely
// Parameter 4 has boundaries [-10,-4] with initial value -8
// Parameter 5 is fixed to 100.
//
Int_t i, ierf, npar,nvpar,nparx,icstat;
Double_t par, we, al, bl;
Double_t eplus,eminus,eparab,globcc,amin,edm,errdef,werr;
TF1 *fnew1;
Double_t *arglist = new Double_t[100];
// Decode string choptin and fill Foption structure
Foption.Quiet = 0;
Foption.Verbose = 0;
Foption.Bound = 0;
Foption.Like = 0;
Foption.W1 = 0;
Foption.Errors = 0;
Foption.Range = 0;
Foption.Gradient= 0;
Foption.Nograph = 0;
Foption.Nostore = 0;
Foption.Plus = 0;
TString opt = option;
opt.ToUpper();
if (opt.Contains("Q")) Foption.Quiet = 1;
if (opt.Contains("V")){Foption.Verbose = 1; Foption.Quiet = 0;}
if (opt.Contains("W")) Foption.W1 = 1;
if (opt.Contains("E")) Foption.Errors = 1;
if (opt.Contains("R")) Foption.Range = 1;
if (opt.Contains("N")) Foption.Nostore = 1;
if (opt.Contains("0")) Foption.Nograph = 1;
if (opt.Contains("+")) Foption.Plus = 1;
xmin = fX[0];
xmax = fX[fNpoints-1];
ymin = fY[0];
ymax = fY[fNpoints-1];
for (i=0;i<fNpoints;i++) {
if (fX[i] < xmin) xmin = fX[i];
if (fX[i] > xmax) xmax = fX[i];
if (fY[i] < ymin) ymin = fY[i];
if (fY[i] > ymax) ymax = fY[i];
}
//*-*- Check if Minuit is initialized and create special functions
if (!gMinuit) gMinuit = new TMinuit(25);
if (!gROOT->GetFunction("gaus")) {
gF1 = new TF1("gaus","gaus",xmin,xmax);
gF1 = new TF1("expo","expo",xmin,xmax);
for (i=0;i<10;i++) gF1 = new TF1(Form("pol%d",i),Form("pol%d",i),xmin,xmax);
}
gMinuit->mncler();
gMinuit->SetObjectFit(this);
//*-*- Get pointer to the function by searching in the list of functions in ROOT
gF1 = gROOT->GetFunction(fname);
if (!gF1) { Printf("Unknown function: %s",fname); return; }
npar = gF1->GetNpar();
if (npar <=0) { Printf("Illegal number of parameters = %d",npar); return; }
//*-*- Check that function has same dimension as histogram
if (gF1->GetNdim() > 1) {
Printf("Error function %s is not 1-D",fname); return; }
//*-*- Is a Fit range specified?
if (Foption.Range) {
gF1->GetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
} else {
gF1->SetRange(xmin, xmax);
xfirst = 1;
xlast = fNpoints;
}
//*-*- If case of a predefined function, then compute initial values of parameters
Int_t special = gF1->GetNumber();
if (special == 100) InitGaus();
else if (special == 200) InitExpo();
else if (special == 299+npar) InitPolynom();
//*-*- Set error criterion for chisquare
arglist[0] = 1;
gMinuit->SetFCN(GraphFitChisquare);
gMinuit->mnexcm("SET ERR",arglist,1,ierf);
//*-*- Some initialisations
if (!Foption.Verbose) {
arglist[0] = -1;
gMinuit->mnexcm("SET PRINT", arglist,1,ierf);
arglist[0] = 0;
gMinuit->mnexcm("SET NOW", arglist,0,ierf);
}
//*-*- Transfer names and initial values of parameters to Minuit
Int_t nfixed = 0;
for (i=0;i<npar;i++) {
par = gF1->GetParameter(i);
gF1->GetParLimits(i,al,bl);
if (al*bl != 0 && al >= bl) {
al = bl = 0;
arglist[nfixed] = i+1;
nfixed++;
}
we = 0.3*TMath::Abs(par);
if (we <= TMath::Abs(par)*1e-6) we = 1;
gMinuit->mnparm(i,gF1->GetParName(i),par,we,al,bl,ierf);
}
if(nfixed > 0)gMinuit->mnexcm("FIX",arglist,nfixed,ierf); // Otto
//*-*- Reset Print level
if (!Foption.Quiet) {
if (Foption.Verbose) { arglist[0] = 2; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
else { arglist[0] = 0; gMinuit->mnexcm("SET PRINT", arglist,1,ierf); }
}
//*-*- Perform minimization
SetBit(kFitInit);
arglist[0] = 5000; //MaxIterations
arglist[1] = 1e-2; //epsilon
gMinuit->mnexcm("MIGRAD",arglist,2,ierf);
if (Foption.Errors) {
gMinuit->mnexcm("HESSE",arglist,0,ierf);
gMinuit->mnexcm("MINOS",arglist,0,ierf);
}
//*-*- Get return status
for (i=0;i<npar;i++) {
gMinuit->mnpout(i,gF1->GetParName(i), par,we,al,bl,ierf);
if (Foption.Errors) werr = we;
else {
gMinuit->mnerrs(i,eplus,eminus,eparab,globcc);
if (eplus > 0 && eminus < 0) werr = 0.5*(eplus-eminus);
else werr = we;
}
gF1->SetParameter(i,par);
gF1->SetParError(i,werr);
}
gMinuit->mnstat(amin,edm,errdef,nvpar,nparx,icstat);
gF1->SetChisquare(amin);
//*-*- Print final values of parameters.
if (!Foption.Quiet) {
if (Foption.Errors) gMinuit->mnprin(4,amin);
else gMinuit->mnprin(3,amin);
}
delete [] arglist;
//*-*- Store fitted function in histogram functions list and draw
if (!Foption.Nostore) {
if (!Foption.Plus) fFunctions->Delete();
fnew1 = new TF1();
gF1->Copy(*fnew1);
fFunctions->Add(fnew1);
fnew1->SetParent(this);
fnew1->Save(xmin,xmax);
if (TestBit(kCanDelete)) return;
if (gPad) gPad->Modified();
}
}
//______________________________________________________________________________
void TGraph::FitPanel()
{
//*-*-*-*-*-*-*Display a panel with all graph fit options*-*-*-*-*-*
//*-* ==========================================
//
// See class TFitPanel for example
if (gPad) {
gROOT->SetSelectedPrimitive(gPad->GetSelected());
gROOT->SetSelectedPad(gPad->GetSelectedPad());
}
TList *lc = (TList*)gROOT->GetListOfCanvases();
if (!lc->FindObject("fitpanelgraph")) {
char cmd[] = "TFitPanelGraph *fitpanel = new TFitPanelGraph("fitpanelgraph","Fit Panel",300,400);";
gInterpreter->ProcessLine(cmd);
return;
}
char cmdupd[] = "fitpanelgraph->SetDefaults(); fitpanelgraph->Show();";
gInterpreter->ProcessLine(cmdupd);
}
//______________________________________________________________________________
Float_t TGraph::GetErrorX(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
Float_t TGraph::GetErrorY(Int_t)
{
// This function is called by GraphFitChisquare.
// It always returns a negative value. Real implementation in TGraphErrors
return -1;
}
//______________________________________________________________________________
TH1F *TGraph::GetHistogram()
{
// Returns a pointer to the histogram used to draw the axis
// Takes into account the two following cases.
// 1- option 'A' was specified in TGraph::Draw. Return fHistogram
// 2- user had called TPad::DrawFrame. return pointer to hframe histogram
if (fHistogram) return fHistogram;
if (!gPad) return 0;
gPad->Modified();
gPad->Update();
if (fHistogram) return fHistogram;
TH1F *h1 = (TH1F*)gPad->GetPrimitive("hframe");
return h1;
}
//______________________________________________________________________________
void TGraph::GetPoint(Int_t i, Float_t &x, Float_t &y)
{
//*-*-*-*-*-*-*-*-*-*-*Get x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0 || i >= fNpoints) return;
if (!fX || !fY) return;
x = fX[i];
y = fY[i];
}
//______________________________________________________________________________
TAxis *TGraph::GetXaxis()
{
// Get x axis of the graph.
if (fHistogram) return fHistogram->GetXaxis();
return 0;
}
//______________________________________________________________________________
TAxis *TGraph::GetYaxis()
{
// Get y axis of the graph.
if (fHistogram) return fHistogram->GetYaxis();
return 0;
}
//______________________________________________________________________________
void GraphFitChisquare(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag)
{
//*-*-*-*-*-*Minimization function for Graphs using a Chisquare method*-*-*-*-*
//*-* =========================================================
Double_t cu,eu,fu,fsum;
Double_t dersum[25], grad[25];
static Double_t eysum[50];
Double_t x[1];
Float_t errormax;
Int_t bin, k, npfits, nparts, part;
TGraph *gr = (TGraph*)gMinuit->GetObjectFit();
Int_t n = gr->GetN();
Float_t *gx = gr->GetX();
Float_t *gy = gr->GetY();
npar = gF1->GetNpar();
Float_t cumin = gy[0];
Float_t cumax = gy[0];
if (flag == 2) for (k=0;k<npar;k++) dersum[k] = gin[k] = 0;
nparts = n/3;
if (nparts == 0) nparts = 1;
if (nparts > 40) nparts = 40;
Float_t fxmin = gF1->GetXmin();
Float_t fxmax = gF1->GetXmax();
Float_t dfx = (fxmax - fxmin)/nparts;
if (gr->TestBit(kFitInit)) {
for (part=0;part<nparts;part++) { eysum[part] = 0;}
}
gF1->InitArgs(x,u);
npfits = 0;
f = 0;
for (bin=0;bin<n;bin++) {
x[0] = gx[bin];
if (Foption.Range) {
if (x[0] < fxmin) continue;
if (x[0] > fxmax) continue;
}
cu = gy[bin];
fu = gF1->EvalPar(x,u);
eu = gr->GetErrorY(bin);
if (Foption.W1) eu = 1;
if (eu < 0) {
part = Int_t((x[0] - fxmin)/dfx);
if (part < 0) part = 0;
if (part >= nparts) part = nparts-1;
if (gr->TestBit(kFitInit)) {
eysum[part] += (cu-fu)*(cu-fu);
if (cu < cumin) cumin = cu;
if (cu > cumax) cumax = cu;
} else {
eu = eysum[part];
}
}
if (flag == 2) {
for (k=0;k<npar;k++) dersum[k] += 1; //should be the derivative
}
npfits++;
if (flag == 2) {
for (k=0;k<npar;k++) grad[k] += dersum[k]*(fu-cu)/eu; dersum[k] = 0;
}
if (eu) fsum = (cu-fu)/eu;
else fsum = cu-fu;
f += fsum*fsum;
}
// make a better error estimate to be used in the next iterations
if (gr->TestBit(kFitInit)) {
gr->ResetBit(kFitInit);
errormax = 0.2*(cumax-cumin);
for (part=0;part<nparts;part++) {
eysum[part] = TMath::Sqrt(eysum[part]);
if (eysum[part] > errormax) eysum[part] = errormax;
if (errormax < 0.2) eysum[part] = 1;
}
}
gF1->SetNumberFitPoints(npfits);
}
//______________________________________________________________________________
void TGraph::InitGaus()
{
//*-*-*-*-*-*Compute Initial values of parameters for a gaussian*-*-*-*-*-*-*
//*-* ===================================================
Double_t allcha, sumx, sumx2, x, val, rms, mean;
Int_t bin;
static Double_t sqrtpi = 2.506628;
//*-*- Compute mean value and RMS of the graph in the given range
allcha = sumx = sumx2 = 0;
for (bin=0;bin<fNpoints;bin++) {
x = fX[bin];
val = fY[bin];
sumx += val*x;
sumx2 += val*x*x;
allcha += val;
}
if (allcha == 0) return;
mean = sumx/allcha;
rms = TMath::Sqrt(sumx2/allcha - mean*mean);
Float_t binwidx = TMath::Abs((fX[fNpoints-1] - fX[0])/fNpoints);
if (rms == 0) rms = 1;
gF1->SetParameter(0,binwidx*allcha/(sqrtpi*rms));
gF1->SetParameter(1,mean);
gF1->SetParameter(2,rms);
}
//______________________________________________________________________________
void TGraph::InitExpo()
{
//*-*-*-*-*-*Compute Initial values of parameters for an exponential*-*-*-*-*
//*-* =======================================================
Double_t constant, slope;
Int_t ifail;
Int_t nchanx = xlast - xfirst + 1;
LeastSquareLinearFit(-nchanx, constant, slope, ifail);
gF1->SetParameter(0,constant);
gF1->SetParameter(1,slope);
}
//______________________________________________________________________________
void TGraph::InitPolynom()
{
//*-*-*-*-*-*Compute Initial values of parameters for a polynom*-*-*-*-*-*-*
//*-* ===================================================
Double_t fitpar[25];
Int_t nchanx = xlast - xfirst + 1;
Int_t npar = gF1->GetNpar();
LeastSquareFit( nchanx, npar, fitpar);
for (Int_t i=0;i<npar;i++) gF1->SetParameter(i, fitpar[i]);
}
//______________________________________________________________________________
void TGraph::LeastSquareFit(Int_t n, Int_t m, Double_t *a)
{
//*-*-*-*-*-*-*-*Least squares lpolynomial fitting without weights*-*-*-*-*-*-*
//*-* =================================================
//
// n number of points to fit
// m number of parameters
// a array of parameters
//
// based on CERNLIB routine LSQ: Translated to C++ by Rene Brun
// (E.Keil. revised by B.Schorr, 23.10.1981.)
//
//
static Double_t zero = 0.;
static Double_t one = 1.;
static Int_t idim = 20;
static Double_t b[400] /* was [20][20] */;
static Int_t i, k, l, ifail;
static Double_t power;
static Double_t da[20], xk, yk;
if (m <= 2) {
LeastSquareLinearFit(n, a[0], a[1], ifail);
return;
}
if (m > idim || m > n) return;
b[0] = Float_t(n);
da[0] = zero;
for (l = 2; l <= m; ++l) {
b[l-1] = zero;
b[m + l*20 - 21] = zero;
da[l-1] = zero;
}
for (k = 0; k < fNpoints; ++k) {
xk = fX[k];
yk = fY[k];
power = one;
da[0] += yk;
for (l = 2; l <= m; ++l) {
power *= xk;
b[l-1] += power;
da[l-1] += power*yk;
}
for (l = 2; l <= m; ++l) {
power *= xk;
b[m + l*20 - 21] += power;
}
}
for (i = 3; i <= m; ++i) {
for (k = i; k <= m; ++k) {
b[k - 1 + (i-1)*20 - 21] = b[k + (i-2)*20 - 21];
}
}
H1LeastSquareSeqnd(m, b, idim, ifail, 1, da);
if (ifail < 0) {
a[0] = fY[0];
for (i=1; i<m; ++i) a[i] = 0;
return;
}
for (i=0; i<m; ++i) a[i] = da[i];
}
//______________________________________________________________________________
void TGraph::LeastSquareLinearFit(Int_t ndata, Double_t &a0, Double_t &a1, Int_t &ifail)
{
//*-*-*-*-*-*-*-*-*-*Least square linear fit without weights*-*-*-*-*-*-*-*-*
//*-* =======================================
//
// extracted from CERNLIB LLSQ: Translated to C++ by Rene Brun
// (added to LSQ by B. Schorr, 15.02.1982.)
//
static Double_t xbar, ybar, x2bar;
static Int_t i, n;
static Double_t xybar;
static Float_t fn, xk, yk;
static Double_t det;
n = TMath::Abs(ndata);
ifail = -2;
xbar = ybar = x2bar = xybar = 0;
for (i = 0; i < fNpoints; ++i) {
xk = fX[i];
yk = fY[i];
if (ndata < 0) {
if (yk <= 0) yk = 1e-9;
yk = TMath::Log(yk);
}
xbar += xk;
ybar += yk;
x2bar += xk*xk;
xybar += xk*yk;
}
fn = Float_t(n);
det = fn*x2bar - xbar*xbar;
ifail = -1;
if (det <= 0) {
a0 = ybar/fn;
a1 = 0;
return;
}
ifail = 0;
a0 = (x2bar*ybar - xbar*xybar) / det;
a1 = (fn*xybar - xbar*ybar) / det;
}
//______________________________________________________________________________
void TGraph::Paint(Option_t *option)
{
//*-*-*-*-*-*-*-*-*-*-*Draw this graph with its current attributes*-*-*-*-*-*-*
//*-* ===========================================
if (strstr(option,"H") || strstr(option,"h")) {
PaintGrapHist(fNpoints, fX, fY, option);
} else {
PaintGraph(fNpoints, fX, fY, option);
}
TObject *f;
if (fFunctions) {
TIter next(fFunctions);
while ((f = (TObject*) next())) {
if (f->IsA() == TF1::Class()) f->Paint("lsame");
else f->Paint();
}
}
}
//______________________________________________________________________________
void TGraph::PaintGraph(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Control function to draw a graph*-*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or X(2) : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or Y(2) : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='F' : A fill area is drawn ('CF' draw a smooth fill area)
//
// chopt='A' : Axis are drawn around the graph
//
// chopt='C' : A smooth Curve is drawn
//
// chopt='*' : A Star is plotted at each point
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart is drawn at each point
//
// chopt='1' : ylow=rwymin
//
//
Int_t OptionLine , OptionAxis , OptionCurve,OptionStar ,OptionMark;
Int_t OptionBar , OptionR , OptionOne;
Int_t OptionFill , OptionZ ,OptionCurveFill;
Int_t i, npt, nloop;
Int_t drawtype;
Float_t xlow, xhigh, ylow, yhigh;
Float_t barxmin, barxmax, barymin, barymax;
Float_t uxmin, uxmax;
Float_t x1, xn, y1, yn;
Float_t dbar, bdelta;
//*-* ______________________________________
if (npoints <= 0) {
Error("PaintGraph", "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("R")) OptionR = 1; else OptionR = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
OptionZ = 0;
//*-* If no "drawing" option is selected and if chopt<>' '
//*-* nothing is done.
if (OptionLine+OptionFill+OptionCurve+OptionStar+OptionMark+OptionBar == 0) {
if (strlen(chopt) == 0) OptionLine=1;
else return;
}
if (OptionStar) SetMarkerStyle(3);
OptionCurveFill = 0;
if (OptionCurve && OptionFill) {
OptionCurveFill = 1;
OptionFill = 0;
}
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- Draw the Axis with a fixed number of division: 510
Float_t rwxmin,rwxmax, rwymin, rwymax, maximum, minimum;
if (OptionAxis) {
rwxmin = rwxmax = x[0];
rwymin = rwymax = y[0];
for (i=1;i<npoints;i++) {
if (x[i] < rwxmin) rwxmin = x[i];
if (x[i] > rwxmax) rwxmax = x[i];
if (y[i] < rwymin) rwymin = y[i];
if (y[i] > rwymax) rwymax = y[i];
}
ComputeRange(rwxmin, rwymin, rwxmax, rwymax); //this is redefined in TGraphErrors
if (rwxmin == rwxmax) rwxmax += 1.;
if (rwymin == rwymax) rwymax += 1.;
Float_t dx = 0.1*(rwxmax-rwxmin);
Float_t dy = 0.1*(rwymax-rwymin);
uxmin = rwxmin - dx;
uxmax = rwxmax + dx;
minimum = rwymin - dy;
maximum = rwymax + dy;
if (fMinimum != -1111) rwymin = minimum = fMinimum;
if (fMaximum != -1111) rwymax = maximum = fMaximum;
if (uxmin < 0 && rwxmin >= 0) {
if (gPad->GetLogx()) uxmin = 0.9*rwxmin;
else uxmin = 0;
}
if (uxmax > 0 && rwxmax <= 0) {
if (gPad->GetLogx()) uxmax = 1.1*rwxmax;
else uxmax = 0;
}
if (minimum < 0 && rwymin >= 0) {
if(gPad->GetLogy()) minimum = 0.9*rwymin;
else minimum = 0;
}
if (maximum > 0 && rwymax <= 0) {
if(gPad->GetLogy()) maximum = 1.1*rwymax;
else maximum = 0;
}
if (minimum <= 0 && gPad->GetLogy()) minimum = 0.001*maximum;
if (uxmin <= 0 && gPad->GetLogx()) {
if (uxmax > 1000) uxmin = 1;
else uxmin = 0.001*uxmax;
}
rwxmin = uxmin;
rwxmax = uxmax;
rwymin = minimum;
rwymax = maximum;
if (fHistogram) {
fHistogram->SetMinimum(rwymin);
fHistogram->SetMaximum(rwymax);
fHistogram->GetXaxis()->SetLimits(rwxmin,rwxmax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
}
//*-*- Create a temporary histogram and fill each channel with the function value
if (!fHistogram) {
fHistogram = new TH1F((char*)GetName(),(char*)GetTitle(),40,rwxmin,rwxmax);
if (!fHistogram) return;
fHistogram->SetMinimum(rwymin);
fHistogram->SetBit(kNoStats);
fHistogram->SetMaximum(rwymax);
fHistogram->GetYaxis()->SetLimits(rwymin,rwymax);
fHistogram->SetDirectory(0);
}
fHistogram->Paint();
}
TF1 *fit = 0;
if (fFunctions) fit = (TF1*)fFunctions->First();
if (fit) {
if (fHistogram) {
fHistogram->PaintStat(0,fit);
} else {
TH1F *hfit = new TH1F("___0","",2,0,1);
hfit->PaintStat(0,fit);
delete hfit;
}
}
rwxmin = gPad->GetUxmin();
rwxmax = gPad->GetUxmax();
rwymin = gPad->GetUymin();
rwymax = gPad->GetUymax();
uxmin = gPad->PadtoX(rwxmin);
uxmax = gPad->PadtoX(rwxmax);
if (fHistogram) {
maximum = fHistogram->GetMaximum();
minimum = fHistogram->GetMinimum();
} else {
maximum = gPad->PadtoY(rwymax);
minimum = gPad->PadtoY(rwymin);
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Draw the graph with a polyline or a fill area
if (OptionLine || OptionFill) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
nloop = npoints;
if (OptionFill && (xn != x1 || yn != y1)) nloop++;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == nloop) {
ComputeLogs(npt, OptionZ);
Int_t bord = gStyle->GetDrawBorder();
if (OptionR) {
if (OptionFill) {
gPad->PaintFillArea(npt,yworkl,xworkl);
if (bord) gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else gPad->PaintPolyLine(npt,yworkl,xworkl);
}
else {
if (OptionFill) {
gPad->PaintFillArea(npt,xworkl,yworkl);
if (bord) gPad->PaintPolyLine(npt,xworkl,yworkl);
}
else gPad->PaintPolyLine(npt,xworkl,yworkl);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
}
}
//*-*- Draw the graph with a smooth Curve. Smoothing via Smooth
if (OptionCurve) {
x1 = x[0];
xn = x[npoints-1];
y1 = y[0];
yn = y[npoints-1];
drawtype = 1;
nloop = npoints;
if (OptionCurveFill) {
drawtype += 1000;
if (xn != x1 || yn != y1) nloop++;
}
if (!OptionR) {
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (yworkl[npt-1] < rwymin || yworkl[npt-1] > rwymax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=0;i<nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype += 10;
npt = 0;
for (i=1;i<=nloop;i++) {
if (i > npoints) {
xwork[npt] = xwork[0]; ywork[npt] = ywork[0];
} else {
if (y[i-1] < minimum || y[i-1] > maximum) continue;
if (x[i-1] < uxmin || x[i-1] > uxmax) continue;
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
ComputeLogs(npt, OptionZ);
if (xworkl[npt-1] < rwxmin || xworkl[npt-1] > rwxmax) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt=1;
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1]; ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=1;i<=nloop;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the graph with a '*' on every points
if (OptionStar) {
SetMarkerStyle(3);
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph with the current polymarker on
//*-*- every points
if (OptionMark) {
npt = 0;
for (i=1;i<=npoints;i++) {
if (y[i-1] >= minimum && y[i-1] <= maximum && x[i-1] >= uxmin && x[i-1] <= uxmax) {
xwork[npt] = x[i-1]; ywork[npt] = y[i-1];
npt++;
}
if (npt == NPMAX || i == npoints) {
ComputeLogs(npt, OptionZ);
if (OptionR) gPad->PaintPolyMarker(npt,yworkl,xworkl);
else gPad->PaintPolyMarker(npt,xworkl,yworkl);
npt = 0;
}
}
}
//*-*- Draw the graph as a bar chart
if (OptionBar) {
if (!OptionR) {
barxmin = x[0];
barxmax = x[0];
for (i=1;i<npoints;i++) {
if (x[i] < barxmin) barxmin = x[i];
if (x[i] > barxmax) barxmax = x[i];
}
bdelta = (barxmax-barxmin)/float(npoints);
}
else {
barymin = y[0];
barymax = y[0];
for (i=1;i<npoints;i++) {
if (y[i] < barymin) barymin = y[i];
if (y[i] > barymax) barymax = y[i];
}
bdelta = (barymax-barymin)/float(npoints);
}
dbar = 0.5*bdelta*gStyle->GetBarWidth();
if (!OptionR) {
for (i=1;i<=npoints;i++) {
xlow = x[i-1] - dbar;
xhigh = x[i-1] + dbar;
yhigh = y[i-1];
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
if (yworkl[0] < gPad->GetUymin()) yworkl[0] = gPad->GetUymin();
if (yworkl[1] < gPad->GetUymin()) continue;
if (yworkl[1] > gPad->GetUymax()) yworkl[0] = gPad->GetUymax();
if (yworkl[0] > gPad->GetUymax()) continue;
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
else {
for (i=1;i<=npoints;i++) {
xhigh = x[i-1];
ylow = y[i-1] - dbar;
yhigh = y[i-1] + dbar;
xlow = TMath::Max((Float_t)0, gPad->GetUxmin());
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1], "B");
}
}
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::PaintGrapHist(Int_t npoints, Float_t *x, Float_t *y, Option_t *chopt)
{
//*-*-*-*-*-*-*-*-*Control function to draw a graphistogram*-*-*-*-*-*-*-*-*-*
//*-* ========================================
//
//
// Draws one dimensional graphs. The aspect of the graph is done
// according to the value of the chopt.
//
// _Input parameters:
//
// npoints : Number of points in X or in Y.
// X(N) or x[1] : X coordinates or (XMIN,XMAX) (WC space).
// Y(N) or y[1] : Y coordinates or (YMIN,YMAX) (WC space).
// chopt : Option.
//
// chopt='R' : Graph is drawn horizontaly, parallel to X axis.
// (default is vertically, parallel to Y axis)
// If option R is selected the user must give:
// 2 values for Y (y[0]=YMIN and y[1]=YMAX)
// N values for X, one for each channel.
// Otherwise the user must give:
// N values for Y, one for each channel.
// 2 values for X (x[0]=XMIN and x[1]=XMAX)
//
// chopt='L' : A simple polyline beetwen every points is drawn
//
// chopt='H' : An Histogram with equidistant bins is drawn
// as a polyline.
//
// chopt='F' : An histogram with equidistant bins is drawn
// as a fill area. Contour is not drawn unless
// chopt='H' is also selected..
//
// chopt='N' : Non equidistant bins (default is equidistant)
// If N is the number of channels array X and Y
// must be dimensionned as follow:
// If option R is not selected (default) then
// the user must give:
// (N+1) values for X (limits of channels).
// N values for Y, one for each channel.
// Otherwise the user must give:
// (N+1) values for Y (limits of channels).
// N values for X, one for each channel.
//
// chopt='F1': Idem as 'F' except that fill area is no more
// reparted arround axis X=0 or Y=0 .
//
// chopt='C' : A smooth Curve is drawn.
//
// chopt='*' : A Star is plotted at the center of each bin.
//
// chopt='P' : Idem with the current marker
//
// chopt='B' : A Bar chart with equidistant bins is drawn as fill
// areas (Contours are drawn).
//
//
static const char *where = "PaintGraphHist";
const Int_t NPMXFA= 99;
Int_t OptionLine , OptionAxis , OptionCurve, OptionStar , OptionMark;
Int_t OptionBar , OptionRot , OptionOne;
Int_t OptionFill , OptionZ;
Int_t OptionHist , OptionBins , OptionMarker;
Int_t i, j, npt;
Int_t drawtype, drawborder, drawbordersav;
Float_t xlow, xhigh, ylow, yhigh;
Float_t wmin, wmax;
Float_t dbar, offset, wminstep;
Float_t delta = 0;
Float_t ylast = 0;
Float_t xi, xi1, xj, xj1, yi1, yi, yj, yj1, xwmin, ywmin;
Int_t first, last, nbins;
Int_t fillarea;
static char choptaxis[10] = " ";
//*-* ______________________________________
if (npoints <= 0) {
Error(where, "illegal number of points (%d)", npoints);
return;
}
TString opt = chopt;
opt.ToUpper();
if(opt.Contains("H")) OptionHist = 1; else OptionHist = 0;
if(opt.Contains("F")) OptionFill = 1; else OptionFill = 0;
if(opt.Contains("C")) OptionCurve= 1; else OptionCurve= 0;
if(opt.Contains("*")) OptionStar = 1; else OptionStar = 0;
if(opt.Contains("R")) OptionRot = 1; else OptionRot = 0;
if(opt.Contains("1")) OptionOne = 1; else OptionOne = 0;
if(opt.Contains("B")) OptionBar = 1; else OptionBar = 0;
if(opt.Contains("N")) OptionBins = 1; else OptionBins = 0;
if(opt.Contains("L")) OptionLine = 1; else OptionLine = 0;
if(opt.Contains("P")) OptionMark = 1; else OptionMark = 0;
if(opt.Contains("A")) OptionAxis = 1; else OptionAxis = 0;
//*-* Set Clipping option
gPad->SetBit(kClipFrame, TestBit(kClipFrame));
//*-*- If necessary the adresses of the vectors are saved in
//*-*- a link area.
OptionZ = 1;
if (OptionStar) SetMarkerStyle(3);
first = 1;
last = npoints;
nbins = last - first + 1;
//*-*- Draw the Axis with a fixed number of division: 510
Float_t baroffset = gStyle->GetBarOffset();
Float_t barwidth = gStyle->GetBarWidth();
Float_t rwxmin = gPad->GetUxmin();
Float_t rwxmax = gPad->GetUxmax();
Float_t rwymin = gPad->GetUymin();
Float_t rwymax = gPad->GetUymax();
Float_t uxmin = gPad->PadtoX(rwxmin);
Float_t uxmax = gPad->PadtoX(rwxmax);
Float_t rounding = (uxmax-uxmin)*1.e-5;
drawborder = gStyle->GetDrawBorder();
if (OptionAxis) {
Int_t nx1, nx2, ndivx, ndivy, ndiv;
choptaxis[0] = 0;
Float_t rwmin = rwxmin;
Float_t rwmax = rwxmax;
ndivx = gStyle->GetNdivisions("X");
ndivy = gStyle->GetNdivisions("Y");
if (ndivx > 1000) {
nx2 = ndivx/100;
nx1 = TMath::Max(1, ndivx%100);
ndivx = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsWNDC());
}
ndiv =TMath::Abs(ndivx);
if (ndivx < 0) strcat(choptaxis, "N");
if (gPad->GetGridx()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogx()) {
rwmin = TMath::Power(10,rwxmin);
rwmax = TMath::Power(10,rwxmax);
strcat(choptaxis, "G");
}
TGaxis *axis = new TGaxis();
axis->SetLineColor(gStyle->GetAxisColor("X"));
axis->SetTextColor(gStyle->GetLabelColor("X"));
axis->SetTextFont(gStyle->GetLabelFont("X"));
axis->SetLabelSize(gStyle->GetLabelSize("X"));
axis->SetLabelOffset(gStyle->GetLabelOffset("X"));
axis->SetTickSize(gStyle->GetTickLength("X"));
axis->PaintAxis(rwxmin,rwymin,rwxmax,rwymin,rwmin,rwmax,ndiv,choptaxis);
choptaxis[0] = 0;
rwmin = rwymin;
rwmax = rwymax;
if (ndivy < 0) {
nx2 = ndivy/100;
nx1 = TMath::Max(1, ndivy%100);
ndivy = 100*nx2 + Int_t(Float_t(nx1)*gPad->GetAbsHNDC());
strcat(choptaxis, "N");
}
ndiv =TMath::Abs(ndivy);
if (gPad->GetGridy()) {
strcat(choptaxis, "W");
}
if (gPad->GetLogy()) {
rwmin = TMath::Power(10,rwymin);
rwmax = TMath::Power(10,rwymax);
strcat(choptaxis,"G");
}
axis->SetLineColor(gStyle->GetAxisColor("Y"));
axis->SetTextColor(gStyle->GetLabelColor("Y"));
axis->SetTextFont(gStyle->GetLabelFont("Y"));
axis->SetLabelSize(gStyle->GetLabelSize("Y"));
axis->SetLabelOffset(gStyle->GetLabelOffset("Y"));
axis->SetTickSize(gStyle->GetTickLength("Y"));
axis->PaintAxis(rwxmin,rwymin,rwxmin,rwymax,rwmin,rwmax,ndiv,choptaxis);
delete axis;
}
//*-*- Set attributes
TAttLine::Modify();
TAttFill::Modify();
TAttMarker::Modify();
//*-*- Min-Max scope
if (!OptionRot) {wmin = x[0]; wmax = x[1];}
else {wmin = y[0]; wmax = y[1];}
if (!OptionBins) delta = (wmax - wmin)/ float(nbins);
//*-*- Draw the histogram with a fill area
if (OptionFill && !OptionCurve) {
fillarea = kTRUE;
if (!OptionRot) {
xwork[0] = wmin;
if (!OptionOne) ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
else ywork[0] = gPad->GetUymin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((j-first+1)*delta);
}
else {
xj1 = x[j]; xj = x[j-1];
if (xj1 < xj) {
if (j != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j];
}
ywork[npt-1] = y[j-1];
ywork[npt] = y[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (j == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
xwork[0] = xwork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++) {
}
else {
ywork[0] = wmin;
if (!OptionOne) xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
else xwork[0] = gPad->GetUxmin();
npt = 2;
for (j=first; j<=last;j++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((j-first+1)*delta);
}
else {
yj1 = y[j]; yj = y[j-1];
if (yj1 < yj) {
if (j != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[j-1]; ywork[npt] = y[j];
}
xwork[npt-1] = x[j-1]; xwork[npt] = x[j-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (j == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
}
continue;
}
if (npt >= NPMXFA) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwork[0];
ComputeLogs(npt, OptionZ);
gPad->PaintFillArea(npt,xworkl,yworkl);
if (drawborder) {
if (!fillarea) yworkl[0] = ylast;
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
fillarea = kFALSE;
}
ylast = yworkl[npt-1];
ywork[0] = ywork[npt-1];
npt = 2;
}
} //endfor (j=first; j<=last;j++)
}
}
//*-*- Draw a standard Histogram (default)
if ((OptionHist) || strlen(chopt) == 0) {
if (!OptionRot) {
xwork[0] = wmin;
// ywork[0] = TMath::Max((Float_t)0,gPad->GetUymin());
ywork[0] = gPad->GetUymin();
ywmin = ywork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
xwork[npt-1] = xwork[npt-2];
xwork[npt] = wmin+((i-first+1)*delta);
}
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i];
}
ywork[npt-1] = y[i-1];
ywork[npt] = y[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
else xwork[npt-2] = TMath::Min(xwork[npt], uxmax);
if (i == last) {
xwork[npt-1] = xwork[npt-2];
ywork[npt-1] = ywmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
else {
ywork[0] = wmin;
xwork[0] = TMath::Max((Float_t)0,gPad->GetUxmin());
xwmin = xwork[0];
npt = 2;
for (i=first; i<=last;i++) {
if (!OptionBins) {
ywork[npt-1] = ywork[npt-2];
ywork[npt] = wmin+((i-first+1)*delta);
}
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1]; ywork[npt] = y[i];
}
xwork[npt-1] = x[i-1]; xwork[npt] = x[i-1];
if (xwork[npt-1] >= uxmin && xwork[npt] <= uxmax+rounding) npt += 2;
if (i == last) {
ywork[npt-1] = ywork[npt-2];
xwork[npt-1] = xwmin;
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
continue;
}
if (npt >= NPMAX) {
ComputeLogs(npt-1, OptionZ);
gPad->PaintPolyLine(npt-1,xworkl,yworkl);
xwork[0] = xwork[npt-2];
ywork[0] = ywork[npt-2];
npt = 2;
}
} //endfor (i=first; i<=last;i++)
}
}
//*-*- Draw the histogram with a smooth Curve. The computing
//*-*- of the smoothing is done by the routine IGRAP1
if (OptionCurve) {
if (!OptionFill) drawtype = 1;
else {
if (!OptionOne) drawtype = 2;
else drawtype = 3;
}
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
ComputeLogs(npt, OptionZ);
if ((yworkl[npt] < rwymin) || (yworkl[npt] > rwymax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
else {
drawtype = drawtype+10;
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wmin+(i-first)*delta+0.5*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
ComputeLogs(npt, OptionZ);
if ((xworkl[npt] < uxmin) || (xworkl[npt] > uxmax)) {
if (npt > 2) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
ComputeLogs(50, OptionZ);
Smooth(50,xworkl,yworkl,drawtype);
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (npt > 1) {
ComputeLogs(npt, OptionZ);
Smooth(npt,xworkl,yworkl,drawtype);
}
}
}
//*-*- Draw the histogram with a simple line
OptionMarker = 0;
if ((OptionStar) || (OptionMark))OptionMarker=1;
if ((OptionMarker) || (OptionLine)) {
wminstep = wmin + 0.5*delta;
if (!OptionRot) {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) xwork[npt-1] = wminstep + (i-first)*delta;
else {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
if (i != last) Error(where, "X must be in increasing order");
else Error(where, "X must have N+1 values with option N");
return;
}
xwork[npt-1] = x[i-1] + 0.5*(x[i]-x[i-1]);
}
if (xwork[npt-1] < uxmin || xwork[npt-1] > uxmax) { npt--; continue;}
ywork[npt-1] = y[i-1];
if ((ywork[npt-1] < rwymin) || (ywork[npt-1] > rwymax)) {
if ((ywork[npt-1] < rwymin)) ywork[npt-1] = rwymin;
if ((ywork[npt-1] > rwymax)) ywork[npt-1] = rwymax;
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
else {
npt = 0;
for (i=first; i<=last;i++) {
npt++;
if (!OptionBins) ywork[npt-1] = wminstep+(i-first)*delta;
else {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
if (i != last) Error(where, "Y must be in increasing order");
else Error(where, "Y must have N+1 values with option N");
return;
}
ywork[npt-1] = y[i-1] + 0.5*(y[i]-y[i-1]);
}
xwork[npt-1] = x[i-1];
if ((xwork[npt-1] < uxmin) || (xwork[npt-1] > uxmax)) {
if (npt > 2) {
if (OptionMarker) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
continue;
}
if (npt >= 50) {
if (OptionMarker) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyMarker(50,xworkl,yworkl);
}
if (OptionLine) {
ComputeLogs(50, OptionZ);
gPad->PaintPolyLine(50,xworkl,yworkl);
}
xwork[0] = xwork[npt-1];
ywork[0] = ywork[npt-1];
npt = 1;
}
} //endfor (i=first; i<=last;i++)
if (OptionMarker && npt > 0) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyMarker(npt,xworkl,yworkl);
}
if (OptionLine != 0 && npt > 1) {
ComputeLogs(npt, OptionZ);
gPad->PaintPolyLine(npt,xworkl,yworkl);
}
}
}
//*-*- Draw the histogram as a bar chart
if (OptionBar) {
if (!OptionBins) { offset = delta*baroffset; dbar = delta*barwidth; }
else {
if (!OptionRot) {
offset = (x[1]-x[0])*baroffset;
dbar = (x[1]-x[0])*barwidth;
} else {
offset = (y[1]-y[0])*baroffset;
dbar = (y[1]-y[0])*barwidth;
}
}
drawbordersav = drawborder;
gStyle->SetDrawBorder(1);
if (!OptionRot) {
xlow = wmin+offset;
xhigh = wmin+offset+dbar;
if (!OptionOne) ylow = TMath::Max((Float_t)0,gPad->GetUymin());
else ylow = gPad->GetUymin();
for (i=first; i<=last;i++) {
yhigh = y[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
if (!OptionBins) {
xlow = xlow+delta;
xhigh = xhigh+delta;
}
else {
if (i < last) {
xi1 = x[i]; xi = x[i-1];
if (xi1 < xi) {
Error(where, "X must be in increasing order");
return;
}
offset = (x[i+1]-x[i])*baroffset;
dbar = (x[i+1]-x[i])*barwidth;
xlow = x[i] + offset;
xhigh = x[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
else {
ylow = wmin + offset;
yhigh = wmin + offset + dbar;
if (!OptionOne) xlow = TMath::Max((Float_t)0,gPad->GetUxmin());
else xlow = gPad->GetUxmin();
for (i=first; i<=last;i++) {
xhigh = x[i-1];
xwork[0] = xlow;
ywork[0] = ylow;
xwork[1] = xhigh;
ywork[1] = yhigh;
ComputeLogs(2, OptionZ);
gPad->PaintBox(xworkl[0],yworkl[0],xworkl[1],yworkl[1]);
gPad->PaintBox(xlow,ylow,xhigh,yhigh);
if (!OptionBins) {
ylow = ylow + delta;
yhigh = yhigh + delta;
}
else {
if (i < last) {
yi1 = y[i]; yi = y[i-1];
if (yi1 < yi) {
Error(where, "Y must be in increasing order");
return;
}
offset = (y[i+1]-y[i])*baroffset;
dbar = (y[i+1]-y[i])*barwidth;
ylow = y[i] + offset;
yhigh = y[i] + offset + dbar;
}
}
} //endfor (i=first; i<=last;i++)
}
gStyle->SetDrawBorder(drawbordersav);
}
gPad->ResetBit(kClipFrame);
}
//______________________________________________________________________________
void TGraph::ComputeLogs(Int_t npoints, Int_t opt)
{
//*-*-*-*-*-*-*-*-*-*-*-*Convert WC from Log scales*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==========================
//
// Take the LOG10 of xwork and ywork according to the value of Options
// and put it in xworkl and yworkl.
//
// npoints : Number of points in xwork and in ywork.
//
for (Int_t i=0;i<npoints;i++) {
xworkl[i] = xwork[i];
yworkl[i] = ywork[i];
if (gPad->GetLogx()) {
if (xworkl[i] > 0) xworkl[i] = TMath::Log10(xworkl[i]);
else xworkl[i] = gPad->GetX1();
}
if (!opt && gPad->GetLogy()) {
if (yworkl[i] > 0) yworkl[i] = TMath::Log10(yworkl[i]);
else yworkl[i] = gPad->GetY1();
}
// if (yworkl[i] > gPad->GetUymax()) yworkl[i] = gPad->GetUymax();
}
}
//______________________________________________________________________________
void TGraph::Print(Option_t *)
{
//*-*-*-*-*-*-*-*-*-*-*Print graph values*-*-*-*-*-*-*-*-*-*-*-*
//*-* ==================
for (Int_t i=0;i<fNpoints;i++) {
printf("x[%d]=%g, y[%d]=%gn",i,fX[i],i,fY[i]);
}
}
//______________________________________________________________________________
void TGraph::SavePrimitive(ofstream &out, Option_t *option)
{
// Save primitive as a C++ statement(s) on output stream out
char quote = '"';
out<<" "<<endl;
if (gROOT->ClassSaved(TGraph::Class())) {
out<<" ";
} else {
out<<" TGraph *";
}
out<<"graph = new TGraph("<<fNpoints<<");"<<endl;
out<<" graph->SetName("<<quote<<GetName()<<quote<<");"<<endl;
out<<" graph->SetTitle("<<quote<<GetTitle()<<quote<<");"<<endl;
SaveFillAttributes(out,"graph",0,1001);
SaveLineAttributes(out,"graph",1,1,1);
SaveMarkerAttributes(out,"graph",1,1,1);
for (Int_t i=0;i<fNpoints;i++) {
out<<" graph->SetPoint("<<i<<","<<fX[i]<<","<<fY[i]<<");"<<endl;
}
out<<" graph->Draw("
<<quote<<option<<quote<<");"<<endl;
}
//______________________________________________________________________________
void TGraph::SetMaximum(Float_t maximum)
{
fMaximum = maximum;
if (fHistogram) fHistogram->SetMaximum(maximum);
}
//______________________________________________________________________________
void TGraph::SetMinimum(Float_t minimum)
{
fMinimum = minimum;
if (fHistogram) fHistogram->SetMinimum(minimum);
}
//______________________________________________________________________________
void TGraph::SetPoint(Int_t i, Float_t x, Float_t y)
{
//*-*-*-*-*-*-*-*-*-*-*Set x and y values for point number i*-*-*-*-*-*-*-*-*
//*-* =====================================
if (i < 0) return;
if (i >= fNpoints) {
// re-allocate the object
Float_t *savex = new Float_t[i+1];
Float_t *savey = new Float_t[i+1];
if (fNpoints > 0) {
memcpy(savex,fX,fNpoints*sizeof(Float_t));
memcpy(savey,fY,fNpoints*sizeof(Float_t));
}
if (fX) delete [] fX;
if (fY) delete [] fY;
fX = savex;
fY = savey;
fNpoints = i+1;
}
fX[i] = x;
fY[i] = y;
}
//______________________________________________________________________________
void TGraph::Smooth(Int_t npoints, Float_t *x, Float_t *y, Int_t drawtype)
{
//*-*-*-*-*-*-*-*-*-*-*-*Smooth a curve given by N points*-*-*-*-*-*-*-*-*-*
//*-* ================================
//
// Underlaying routine for Draw based on the CERN GD3 routine TVIPTE
//
// Author - Marlow etc. Modified by - P. Ward Date - 3.10.1973
//
// This routine draws a smooth tangentially continuous curve through
// the sequence of data points P(I) I=1,N where P(I)=(X(I),Y(I))
// the curve is approximated by a polygonal arc of short vectors .
// the data points can represent open curves, P(1) != P(N) or closed
// curves P(2) == P(N) . If a tangential discontinuity at P(I) is
// required , then set P(I)=P(I+1) . loops are also allowed .
//
// Reference Marlow and Powell,Harwell report No.R.7092.1972
// MCCONALOGUE,Computer Journal VOL.13,NO4,NOV1970PP392 6
//
// _Input parameters:
//
// npoints : Number of data points.
// x : Abscissa
// y : Ordinate
//
//
// delta is the accuracy required in constructing the curve.
// if it is zero then the routine calculates a value other-
// wise it uses this value. (default is 0.0)
//
//
Int_t i, k, kp, km, NpointsMax, banksize, n2, npt;
Int_t maxiterations, finished;
Int_t jtype, ktype, closed;
Float_t sxmin, sxmax, symin, symax;
Float_t delta;
Float_t xorg, yorg;
Float_t ratio_signs, xratio, yratio;
Int_t flgic, flgis;
Int_t iw, loptx;
Float_t P1, P2, P3, P4, P5, P6;
Float_t W1, W2, W3;
Float_t A, B, C, R, S, T, Z;
Float_t CO, SO, CT, ST, CTU, STU, XNT;
Float_t DX1, DY1, DX2, DY2, DK1, DK2;
Float_t XO, YO, DX, DY, XT, YT;
Float_t XA, XB, YA, YB;
Float_t U1, U2, U3, TJ;
Float_t CC, ERR;
Float_t SB, STH;
Float_t wsign, tsquare, tcube;
C = T = CO = SO = CT = ST = CTU = STU = DX1 = DY1 = DX2 = DY2 = 0;
XT = YT = XA = XB = YA = YB = U1 = U2 = U3 = TJ = SB = 0;
//*-* ______________________________________
NpointsMax = npoints*10;
n2 = NpointsMax-2;
banksize = n2;
Float_t *qlx = new Float_t[NpointsMax];
Float_t *qly = new Float_t[NpointsMax];
if (!qlx || !qly) {
Error("Smooth", "not enough space in memory");
return;
}
//*-*- Decode the type of curve according to
//*-*- chopt of IGHIST.
//*-*- ('S', 'SA', 'SA1' ,'XS', 'XSA', or 'XSA1')
if (drawtype >= 1000) drawtype -= 1000;
loptx = kFALSE;
jtype = drawtype-10;
if (jtype > 0) { ktype = jtype; loptx = kTRUE; }
else ktype = drawtype;
Float_t ruxmin = gPad->GetUxmin();
Float_t ruymin = gPad->GetUymin();
if (ktype == 3) {
xorg = ruxmin;
yorg = ruymin;
} else {
xorg = TMath::Max((Float_t)0,ruxmin);
yorg = TMath::Max((Float_t)0,ruymin);
}
maxiterations = 20;
delta = 0.00055;
//*-*- Scale data to the range 0-ratio_signs in X, 0-1 in Y
//*-*- where ratio_signs is the ratio between the number of changes
//*-*- of sign in Y divided by the number of changes of sign in X
sxmin = x[0];
sxmax = x[0];
symin = y[0];
symax = y[0];
Float_t six = 1;
Float_t siy = 1;
for (i=1;i<npoints;i++) {
if (i > 1) {
if ((x[i]-x[i-1])*(x[i-1]-x[i-2]) < 0) six++;
if ((y[i]-y[i-1])*(y[i-1]-y[i-2]) < 0) siy++;
}
if (x[i] < sxmin) sxmin = x[i];
if (x[i] > sxmax) sxmax = x[i];
if (y[i] < symin) symin = y[i];
if (y[i] > symax) symax = y[i];
}
closed = 0;
Float_t dx1n = TMath::Abs(x[npoints-1]-x[0]);
Float_t dy1n = TMath::Abs(y[npoints-1]-y[0]);
if (dx1n < 0.01*(sxmax-sxmin) && dy1n < 0.01*(symax-symin)) closed = 1;
if (sxmin == sxmax) xratio = 1;
else {
if (six > 1) ratio_signs = siy/six;
else ratio_signs = 20;
xratio = ratio_signs/(sxmax-sxmin);
}
if (symin == symax) yratio = 1;
else yratio = 1/(symax-symin);
qlx[0] = x[0];
qly[0] = y[0];
for (i=0;i<npoints;i++) {
x[i] = (x[i]-sxmin)*xratio;
y[i] = (y[i]-symin)*yratio;
}
//*-*- finished is minus one if we must draw a straight line from P(k-1)
//*-*- to P(k). finished is one if the last call to IPL has < N2
//*-*- points. finished is zero otherwise. npt counts the X and Y
//*-*- coordinates in work . When npt=N2 a call to IPL is made.
finished = 0;
npt = 1;
k = 1;
//*-*- Convert coordinates back to original system
//*-*- Separate the set of data points into arcs P(k-1),P(k).
//*-*- Calculate the direction cosines. first consider whether
//*-*- there is a continuous tangent at the endpoints.
if (!closed) {
if (x[0] != x[npoints-1] || y[0] != y[npoints-1]) goto L40;
if (x[npoints-2] == x[npoints-1] && y[npoints-2] == y[npoints-1]) goto L40;
if (x[0] == x[1] && y[0] == y[1]) goto L40;
}
flgic = kFALSE;
flgis = kTRUE;
//*-*- flgic is true if the curve is open and false if it is closed.
//*-*- flgis is true in the main loop, but is false if there is
//*-*- a deviation from the main loop.
km = npoints - 1;
//*-*- Calculate direction cosines at P(1) using P(N-1),P(1),P(2).
goto L100;
L40:
flgic = kTRUE;
flgis = kFALSE;
//*-*- Skip excessive consecutive equal points.
L50:
if (k >= npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
k++;
if (x[k-1] == x[k-2] && y[k-1] == y[k-2]) goto L50;
L60:
km = k-1;
if (k > npoints) {
finished = 1; //*-*- Prepare to clear out remaining short vectors before returning
if (npt > 1) goto L310;
goto L390;
}
if (k < npoints) goto L90;
if (!flgic) { kp = 2; goto L130;}
L80:
if (flgis) goto L150;
//*-*- Draw a straight line from P(k-1) to P(k).
finished = -1;
goto L170;
//*-*- Test whether P(k) is a cusp.
L90:
if (x[k-1] == x[k] && y[k-1] == y[k]) goto L80;
L100:
kp = k+1;
goto L130;
//*-*- Branch if the next section of the curve begins at a cusp.
L110:
if (!flgis) goto L50;
//*-*- Carry forward the direction cosines from the previous arc.
L120:
CO = CT;
SO = ST;
k++;
goto L60;
//*-*- Calculate the direction cosines at P(k). If k=1 then
//*-*- N-1 is used for k-1. If k=N then 2 is used for k+1.
//*-*- direction cosines at P(k) obtained from P(k-1),P(k),P(k+1).
L130:
DX1 = x[k-1] - x[km-1];
DY1 = y[k-1] - y[km-1];
DK1 = DX1*DX1 + DY1*DY1;
DX2 = x[kp-1] - x[k-1];
DY2 = y[kp-1] - y[k-1];
DK2 = DX2*DX2 + DY2*DY2;
CTU = DX1*DK2 + DX2*DK1;
STU = DY1*DK2 + DY2*DK1;
XNT = CTU*CTU + STU*STU;
//*-*- If both ctu and stu are zero,then default.This can
//*-*- occur when P(k)=P(k+1). I.E. A loop.
if (XNT < 1.E-25) {
CTU = DY1;
STU =-DX1;
XNT = DK1;
}
//*-*- Normalise direction cosines.
CT = CTU/TMath::Sqrt(XNT);
ST = STU/TMath::Sqrt(XNT);
if (flgis) goto L160;
//*-*- Direction cosines at P(k-1) obtained from P(k-1),P(k),P(k+1).
W3 = 2*(DX1*DY2-DX2*DY1);
CO = CTU+W3*DY1;
SO = STU-W3*DX1;
XNT = 1/TMath::Sqrt(CO*CO+SO*SO);
CO = CO*XNT;
SO = SO*XNT;
flgis = kTRUE;
goto L170;
//*-*- Direction cosines at P(k) obtained from P(k-2),P(k-1),P(k).
L150:
W3 = 2*(DX1*DY2-DX2*DY1);
CT = CTU-W3*DY2;
ST = STU+W3*DX2;
XNT = 1/TMath::Sqrt(CT*CT+ST*ST);
CT = CT*XNT;
ST = ST*XNT;
flgis = kFALSE;
goto L170;
L160:
if (k <= 1) goto L120;
//*-*- For the arc between P(k-1) and P(k) with direction cosines CO,
//*-*- SO and CT,ST respectively, calculate the coefficients of the
//*-*- parametric cubic represented by X(T) and Y(T) where
//*-*- X(T)=XA*T**3 + XB*T**2 + CO*T + XO
//*-*- Y(T)=YA*T**3 + YB*T**2 + SO*T + YO
L170:
XO = x[k-2];
YO = y[k-2];
DX = x[k-1] - XO;
DY = y[k-1] - YO;
//*-*- Initialise the values of X(TI),Y(TI) in XT and YT respectively.
XT = XO;
YT = YO;
if (finished < 0) { //*-*- Draw a straight line between (XO,YO) and (XT,YT)
XT += DX;
YT += DY;
goto L300;
}
C = DX*DX+DY*DY;
A = CO+CT;
B = SO+ST;
R = DX*A+DY*B;
T = C*6/(TMath::Sqrt(R*R+2*(7-CO*CT-SO*ST)*C)+R);
tsquare = T*T;
tcube = T*tsquare;
XA = (A*T-2*DX)/tcube;
XB = (3*DX-(CO+A)*T)/tsquare;
YA = (B*T-2*DY)/tcube;
YB = (3*DY-(SO+B)*T)/tsquare;
//*-*- If the curve is close to a straight line then use a straight
//*-*- line between (XO,YO) and (XT,YT).
if (.75*TMath::Max(TMath::Abs(DX*SO-DY*CO),TMath::Abs(DX*ST-DY*CT)) <= delta) {
finished = -1;
XT += DX;
YT += DY;
goto L300;
}
//*-*- Calculate a set of values 0 == T(0).LTCT(1) < ... < T(M)=TC
//*-*- such that polygonal arc joining X(T(J)),Y(T(J)) (J=0,1,..M)
//*-*- is within the required accuracy of the curve
TJ = 0;
U1 = YA*XB-YB*XA;
U2 = YB*CO-XB*SO;
U3 = SO*XA-YA*CO;
//*-*- Given T(J), calculate T(J+1). The values of X(T(J)),
//*-*- Y(T(J)) T(J) are contained in XT,YT and TJ respectively.
L180:
S = T - TJ;
iw = -2;
//*-*- Define iw here later.
P1 = (2*U1)*TJ-U3;
P2 = (U1*TJ-U3)*3*TJ+U2;
P3 = 3*TJ*YA+YB;
P4 = (P3+YB)*TJ+SO;
P5 = 3*TJ*XA+XB;
P6 = (P5+XB)*TJ+CO;
//*-*- Test D(TJ,THETA). A is set to (Y(TJ+S)-Y(TJ))/S.B is
//*-*- set to (X(TJ+S)-X(TJ))/S.
CC = 0.8209285;
ERR = 0.1209835;
L190:
iw -= 2;
L200:
A = (S*YA+P3)*S+P4;
B = (S*XA+P5)*S+P6;
//*-*- Set Z to PSI(D/delta)-CC.
W1 = -S*(S*U1+P1);
W2 = S*S*U1-P2;
W3 = 1.5*W1+W2;
//*-*- Set the estimate of (THETA-TJ)/S.Then set the numerator
//*-*- of the expression (EQUATION 4.4)/S. Then set the square
//*-*- of D(TJ,TJ+S)/delta. Then replace Z by PSI(D/delta)-CC.
if (W3 > 0) wsign = TMath::Abs(W1);
else wsign = -TMath::Abs(W1);
STH = 0.5+wsign/(3.4*TMath::Abs(W1)+5.2*TMath::Abs(W3));
Z = S*STH*(S-S*STH)*(W1*STH+W1+W2);
Z = Z*Z/((A*A+B*B)*(delta*delta));
Z = (Z+2.642937)*Z/((.3715652*Z+3.063444)*Z+.2441889)-CC;
//*-*- Branch if Z has been calculated
if (iw > 0) goto L250;
if (Z > ERR) goto L240;
goto L220;
L210:
iw -= 2;
L220:
if (iw+2 == 0) goto L190;
if (iw+2 > 0) goto L290;
//*-*- Last part of arc.
L230:
XT = x[k-1];
YT = y[k-1];
S = 0;
goto L300;
//*-*- Z(S). find a value of S where 0 <= S <= SB such that
//*-*- TMath::Abs(Z(S)) < ERR
L240:
kp = 0;
C = Z;
SB = S;
L250:
Zero(kp,0,SB,ERR,S,Z,maxiterations);
if (kp == 2) goto L210;
if (kp > 2) {
Error("Smooth", "Attempt to plot outside plot limits");
goto L230;
}
if (iw > 0) goto L200;
//*-*- Set Z=Z(S) for S=0.
if (iw < 0) {
Z = -CC;
iw = 0;
goto L250;
}
//*-*- Set Z=Z(S) for S=SB.
Z = C;
iw = 1;
goto L250;
//*-*- Update TJ,XT and YT.
L290:
XT = XT + S*B;
YT = YT + S*A;
TJ = S + TJ;
//*-*- Convert coordinates to original system
L300:
qlx[npt] = sxmin + XT/xratio;
qly[npt] = symin + YT/yratio;
npt++;
//*-*- If a fill area must be drawn and if the banks LX and
//*-*- LY are too small they are enlarged in order to draw
//*-*- the filled area in one go.
if (npt < banksize) goto L320;
if (drawtype >= 1000 || ktype > 1) {
Int_t newsize = banksize + n2;
Float_t *qtemp = new Float_t[banksize];
for (i=0;i<banksize;i++) qtemp[i] = qlx[i];
delete [] qlx;
qlx = new Float_t[newsize];
for (i=0;i<banksize;i++) qlx[i] = qtemp[i];
for (i=0;i<banksize;i++) qtemp[i] = qly[i];
delete [] qly;
qly = new Float_t[newsize];
for (i=0;i<banksize;i++) qly[i] = qtemp[i];
delete [] qtemp;
banksize = newsize;
goto L320;
}
//*-*- Draw the graph
L310:
if (drawtype >= 1000) {
gPad->PaintFillArea(npt,qlx,qly, "B");
}
else {
if (ktype > 1) {
if (!loptx) {
qlx[npt] = qlx[npt-1];
qlx[npt+1] = qlx[0];
qly[npt] = yorg;
qly[npt+1] = yorg;
}
else {
qlx[npt] = xorg;
qlx[npt+1] = xorg;
qly[npt] = qly[npt-1];
qly[npt+1] = qly[0];
}
gPad->PaintFillArea(npt+2,qlx,qly);
}
gPad->PaintPolyLine(npt,qlx,qly);
}
npt = 1;
qlx[0] = sxmin + XT/xratio;
qly[0] = symin + YT/yratio;
L320:
if (finished > 0) goto L390;
if (finished < 0) { finished = 0; goto L110;}
if (S > 0) goto L180;
goto L110;
//*-*- Convert coordinates back to original system
L390:
for (i=0;i<npoints;i++) {
x[i] = sxmin + x[i]/xratio;
y[i] = symin + y[i]/yratio;
}
delete [] qlx;
delete [] qly;
}
//______________________________________________________________________________
void TGraph::Streamer(TBuffer &b)
{
// Stream an object of class TGraph.
if (b.IsReading()) {
b.ReadVersion(); //Version_t v = b.ReadVersion();
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b >> fNpoints;
fX = new Float_t[fNpoints];
fY = new Float_t[fNpoints];
b.ReadFastArray(fX,fNpoints);
b.ReadFastArray(fY,fNpoints);
b >> fFunctions;
b >> fHistogram;
if (fHistogram) fHistogram->SetDirectory(0);
b >> fMinimum;
b >> fMaximum;
} else {
b.WriteVersion(TGraph::IsA());
TNamed::Streamer(b);
TAttLine::Streamer(b);
TAttFill::Streamer(b);
TAttMarker::Streamer(b);
b << fNpoints;
b.WriteFastArray(fX,fNpoints);
b.WriteFastArray(fY,fNpoints);
b << fFunctions;
b << (TObject *)fHistogram;
b << fMinimum;
b << fMaximum;
}
}
//______________________________________________________________________________
void TGraph::Zero(Int_t &k,Float_t AZ,Float_t BZ,Float_t E2,Float_t &X,Float_t &Y
,Int_t maxiterations)
{
//*-*-*-*-*-*-*-*-*-*-*-*Find zero of a continuous function*-*-*-*-*-*-*-*-*-*
//*-* ==================================
//
// Underlaying routine for PaintGraph
// This function finds a real zero of the continuous real
// function Y(X) in a given interval (A,B). See accompanying
// notes for details of the argument list and calling sequence
//
//
static Float_t A, B, YA, ytest, Y1, X1, H;
static Int_t J1, IT, J3, J2;
Float_t YB, X2;
YB = 0;
//*-*______________________________________
//*-*- Calculate Y(X) at X=AZ.
if (k <= 0) {
A = AZ;
B = BZ;
X = A;
J1 = 1;
IT = 1;
k = J1;
return;
}
//*-*- Test whether Y(X) is sufficiently small.
if (TMath::Abs(Y) <= E2) { k = 2; return; }
//*-*- Calculate Y(X) at X=BZ.
if (J1 == 1) {
YA = Y;
X = B;
J1 = 2;
return;
}
//*-*- Test whether the signs of Y(AZ) and Y(BZ) are different.
//*-*- if not, begin the binary subdivision.
if (J1 != 2) goto L100;
if (YA*Y < 0) goto L120;
X1 = A;
Y1 = YA;
J1 = 3;
H = B - A;
J2 = 1;
X2 = A + 0.5*H;
J3 = 1;
IT++; //*-*- Check whether (maxiterations) function values have been calculated.
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Test whether a bracket has been found .
//*-*- If not,continue the search
L100:
if (J1 > 3) goto L170;
if (YA*Y >= 0) {
if (J3 >= J2) {
H = 0.5*H; J2 = 2*J2;
A = X1; YA = Y1; X2 = A + 0.5*H; J3 = 1;
}
else {
A = X; YA = Y; X2 = X + H; J3++;
}
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- The first bracket has been found.calculate the next X by the
//*-*- secant method based on the bracket.
L120:
B = X;
YB = Y;
J1 = 4;
L130:
if (TMath::Abs(YA) > TMath::Abs(YB)) { X1 = A; Y1 = YA; X = B; Y = YB; }
else { X1 = B; Y1 = YB; X = A; Y = YA; }
//*-*- Use the secant method based on the function values Y1 and Y.
//*-*- check that X2 is inside the interval (A,B).
L150:
X2 = X-Y*(X-X1)/(Y-Y1);
X1 = X;
Y1 = Y;
ytest = 0.5*TMath::Min(TMath::Abs(YA),TMath::Abs(YB));
if ((X2-A)*(X2-B) < 0) {
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
}
//*-*- Calculate the next value of X by bisection . Check whether
//*-*- the maximum accuracy has been achieved.
L160:
X2 = 0.5*(A+B);
ytest = 0;
if ((X2-A)*(X2-B) >= 0) { k = 2; return; }
IT++;
if (IT >= maxiterations) k = J1;
else X = X2;
return;
//*-*- Revise the bracket (A,B).
L170:
if (J1 != 4) return;
if (YA*Y < 0) { B = X; YB = Y; }
else { A = X; YA = Y; }
//*-*- Use ytest to decide the method for the next value of X.
if (ytest <= 0) goto L130;
if (TMath::Abs(Y)-ytest <= 0) goto L150;
goto L160;
}